Pick-and-Mix Information Operators for Probabilistic ODE Solvers
Paper and Code
Oct 20, 2021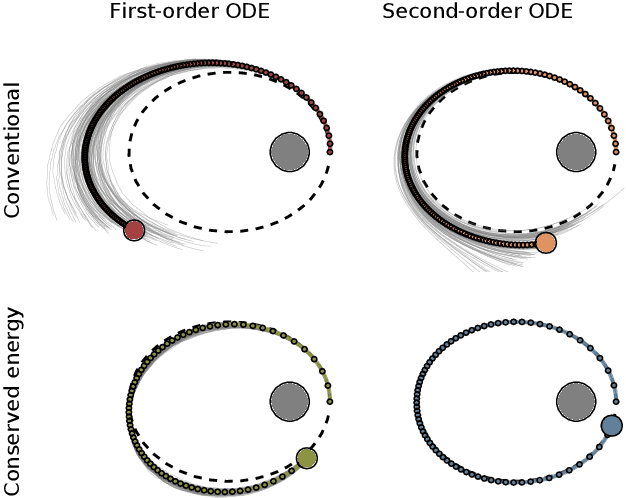

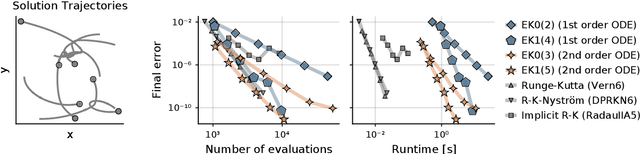
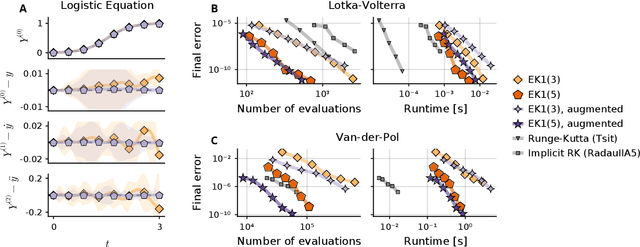
Probabilistic numerical solvers for ordinary differential equations compute posterior distributions over the solution of an initial value problem via Bayesian inference. In this paper, we leverage their probabilistic formulation to seamlessly include additional information as general likelihood terms. We show that second-order differential equations should be directly provided to the solver, instead of transforming the problem to first order. Additionally, by including higher-order information or physical conservation laws in the model, solutions become more accurate and more physically meaningful. Lastly, we demonstrate the utility of flexible information operators by solving differential-algebraic equations. In conclusion, the probabilistic formulation of numerical solvers offers a flexible way to incorporate various types of information, thus improving the resulting solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge