ViViT: Curvature access through the generalized Gauss-Newton's low-rank structure
Paper and Code
Jun 04, 2021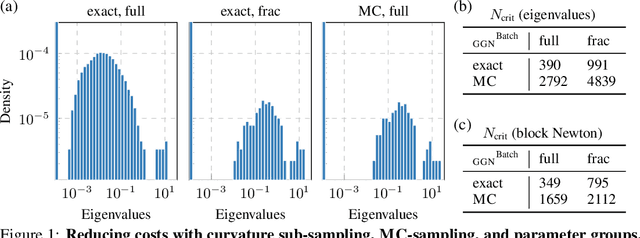
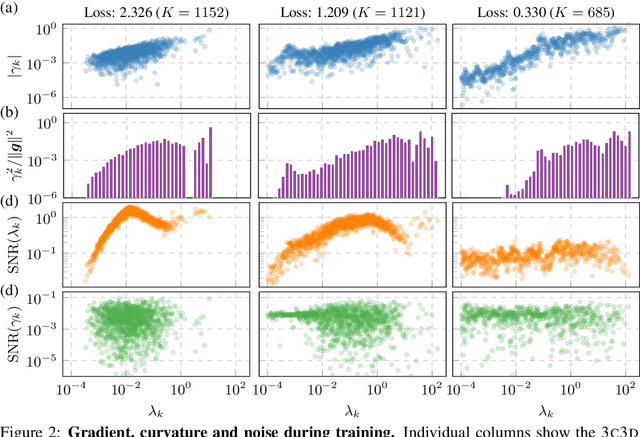
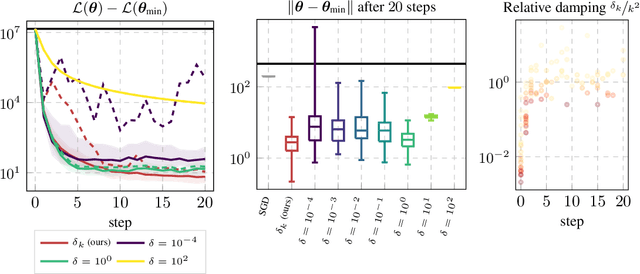
Curvature in form of the Hessian or its generalized Gauss-Newton (GGN) approximation is valuable for algorithms that rely on a local model for the loss to train, compress, or explain deep networks. Existing methods based on implicit multiplication via automatic differentiation or Kronecker-factored block diagonal approximations do not consider noise in the mini-batch. We present ViViT, a curvature model that leverages the GGN's low-rank structure without further approximations. It allows for efficient computation of eigenvalues, eigenvectors, as well as per-sample first- and second-order directional derivatives. The representation is computed in parallel with gradients in one backward pass and offers a fine-grained cost-accuracy trade-off, which allows it to scale. As examples for ViViT's usefulness, we investigate the directional gradients and curvatures during training, and how noise information can be used to improve the stability of second-order methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge