Accelerating Generalized Linear Models by Trading off Computation for Uncertainty

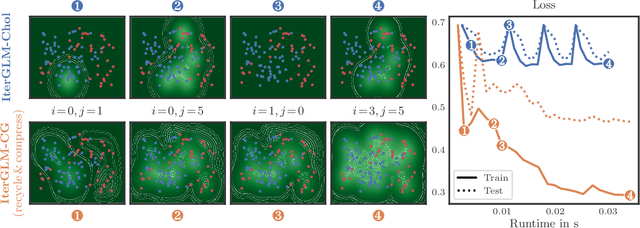
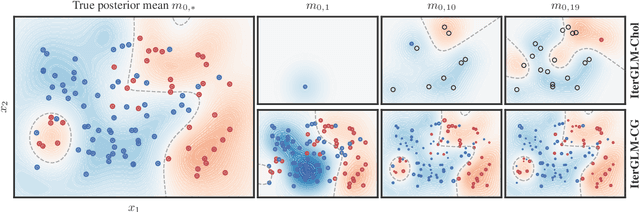
Bayesian Generalized Linear Models (GLMs) define a flexible probabilistic framework to model categorical, ordinal and continuous data, and are widely used in practice. However, exact inference in GLMs is prohibitively expensive for large datasets, thus requiring approximations in practice. The resulting approximation error adversely impacts the reliability of the model and is not accounted for in the uncertainty of the prediction. In this work, we introduce a family of iterative methods that explicitly model this error. They are uniquely suited to parallel modern computing hardware, efficiently recycle computations, and compress information to reduce both the time and memory requirements for GLMs. As we demonstrate on a realistically large classification problem, our method significantly accelerates training by explicitly trading off reduced computation for increased uncertainty.