Black-Box Variational Inference Converges

We provide the first convergence guarantee for full black-box variational inference (BBVI), also known as Monte Carlo variational inference. While preliminary investigations worked on simplified versions of BBVI (e.g., bounded domain, bounded support, only optimizing for the scale, and such), our setup does not need any such algorithmic modifications. Our results hold for log-smooth posterior densities with and without strong log-concavity and the location-scale variational family. Also, our analysis reveals that certain algorithm design choices commonly employed in practice, particularly, nonlinear parameterizations of the scale of the variational approximation, can result in suboptimal convergence rates. Fortunately, running BBVI with proximal stochastic gradient descent fixes these limitations, and thus achieves the strongest known convergence rate guarantees. We evaluate this theoretical insight by comparing proximal SGD against other standard implementations of BBVI on large-scale Bayesian inference problems.

Practical and Matching Gradient Variance Bounds for Black-Box Variational Bayesian Inference

Understanding the gradient variance of black-box variational inference (BBVI) is a crucial step for establishing its convergence and developing algorithmic improvements. However, existing studies have yet to show that the gradient variance of BBVI satisfies the conditions used to study the convergence of stochastic gradient descent (SGD), the workhorse of BBVI. In this work, we show that BBVI satisfies a matching bound corresponding to the $ABC$ condition used in the SGD literature when applied to smooth and quadratically-growing log-likelihoods. Our results generalize to nonlinear covariance parameterizations widely used in the practice of BBVI. Furthermore, we show that the variance of the mean-field parameterization has provably superior dimensional dependence.

Markov Chain Score Ascent: A Unifying Framework of Variational Inference with Markovian Gradients

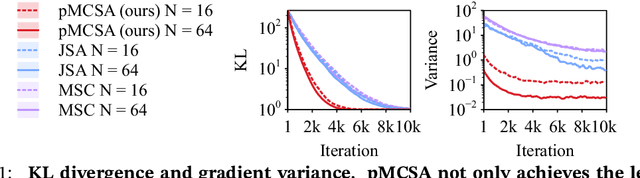
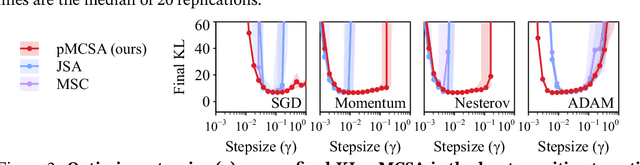
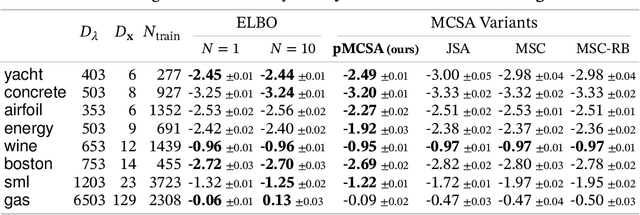
Minimizing the inclusive Kullback-Leibler (KL) divergence with stochastic gradient descent (SGD) is challenging since its gradient is defined as an integral over the posterior. Recently, multiple methods have been proposed to run SGD with biased gradient estimates obtained from a Markov chain. This paper provides the first non-asymptotic convergence analysis of these methods by establishing their mixing rate and gradient variance. To do this, we demonstrate that these methods-which we collectively refer to as Markov chain score ascent (MCSA) methods-can be cast as special cases of the Markov chain gradient descent framework. Furthermore, by leveraging this new understanding, we develop a novel MCSA scheme, parallel MCSA (pMCSA), that achieves a tighter bound on the gradient variance. We demonstrate that this improved theoretical result translates to superior empirical performance.