Markov Chain Score Ascent: A Unifying Framework of Variational Inference with Markovian Gradients
Paper and Code
Jun 13, 2022
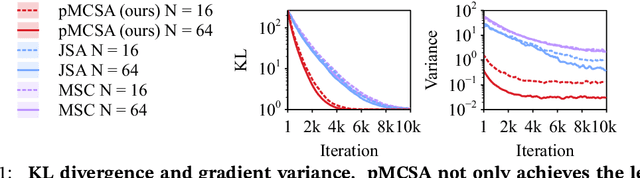
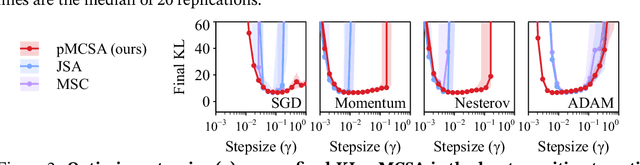
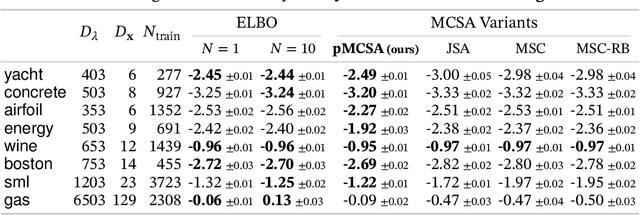
Minimizing the inclusive Kullback-Leibler (KL) divergence with stochastic gradient descent (SGD) is challenging since its gradient is defined as an integral over the posterior. Recently, multiple methods have been proposed to run SGD with biased gradient estimates obtained from a Markov chain. This paper provides the first non-asymptotic convergence analysis of these methods by establishing their mixing rate and gradient variance. To do this, we demonstrate that these methods-which we collectively refer to as Markov chain score ascent (MCSA) methods-can be cast as special cases of the Markov chain gradient descent framework. Furthermore, by leveraging this new understanding, we develop a novel MCSA scheme, parallel MCSA (pMCSA), that achieves a tighter bound on the gradient variance. We demonstrate that this improved theoretical result translates to superior empirical performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge