Self-supervised Equality Embedded Deep Lagrange Dual for Approximate Constrained Optimization

Conventional solvers are often computationally expensive for constrained optimization, particularly in large-scale and time-critical problems. While this leads to a growing interest in using neural networks (NNs) as fast optimal solution approximators, incorporating the constraints with NNs is challenging. In this regard, we propose deep Lagrange dual with equality embedding (DeepLDE), a framework that learns to find an optimal solution without using labels. To ensure feasible solutions, we embed equality constraints into the NNs and train the NNs using the primal-dual method to impose inequality constraints. Furthermore, we prove the convergence of DeepLDE and show that the primal-dual learning method alone cannot ensure equality constraints without the help of equality embedding. Simulation results on convex, non-convex, and AC optimal power flow (AC-OPF) problems show that the proposed DeepLDE achieves the smallest optimality gap among all the NN-based approaches while always ensuring feasible solutions. Furthermore, the computation time of the proposed method is about 5 to 250 times faster than DC3 and the conventional solvers in solving constrained convex, non-convex optimization, and/or AC-OPF.

Markov Chain Score Ascent: A Unifying Framework of Variational Inference with Markovian Gradients

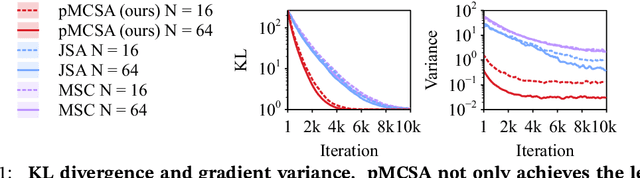
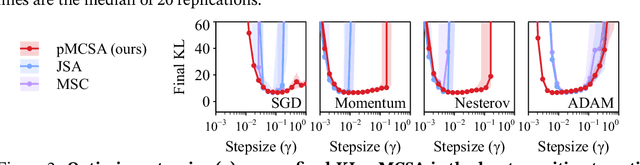
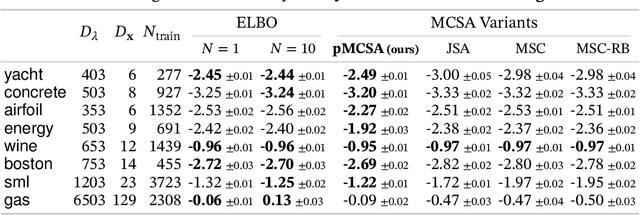
Minimizing the inclusive Kullback-Leibler (KL) divergence with stochastic gradient descent (SGD) is challenging since its gradient is defined as an integral over the posterior. Recently, multiple methods have been proposed to run SGD with biased gradient estimates obtained from a Markov chain. This paper provides the first non-asymptotic convergence analysis of these methods by establishing their mixing rate and gradient variance. To do this, we demonstrate that these methods-which we collectively refer to as Markov chain score ascent (MCSA) methods-can be cast as special cases of the Markov chain gradient descent framework. Furthermore, by leveraging this new understanding, we develop a novel MCSA scheme, parallel MCSA (pMCSA), that achieves a tighter bound on the gradient variance. We demonstrate that this improved theoretical result translates to superior empirical performance.