Chase Tymms
Look-Ahead Acquisition Functions for Bernoulli Level Set Estimation
Mar 18, 2022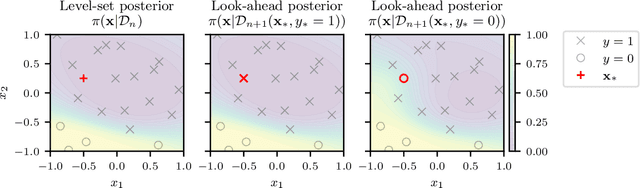
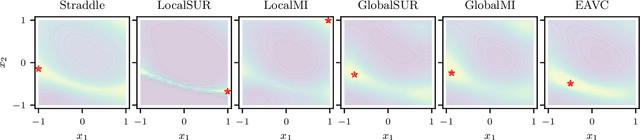
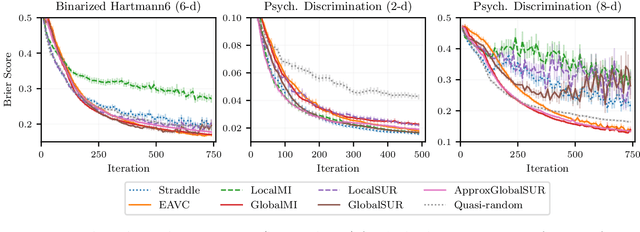

Abstract:Level set estimation (LSE) is the problem of identifying regions where an unknown function takes values above or below a specified threshold. Active sampling strategies for efficient LSE have primarily been studied in continuous-valued functions. Motivated by applications in human psychophysics where common experimental designs produce binary responses, we study LSE active sampling with Bernoulli outcomes. With Gaussian process classification surrogate models, the look-ahead model posteriors used by state-of-the-art continuous-output methods are intractable. However, we derive analytic expressions for look-ahead posteriors of sublevel set membership, and show how these lead to analytic expressions for a class of look-ahead LSE acquisition functions, including information-based methods. Benchmark experiments show the importance of considering the global look-ahead impact on the entire posterior. We demonstrate a clear benefit to using this new class of acquisition functions on benchmark problems, and on a challenging real-world task of estimating a high-dimensional contrast sensitivity function.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge