Rapid Grassmannian Averaging with Chebyshev Polynomials

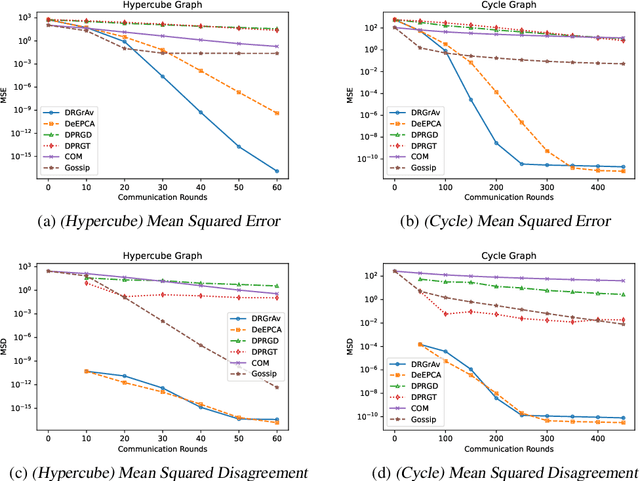
We propose new algorithms to efficiently average a collection of points on a Grassmannian manifold in both the centralized and decentralized settings. Grassmannian points are used ubiquitously in machine learning, computer vision, and signal processing to represent data through (often low-dimensional) subspaces. While averaging these points is crucial to many tasks (especially in the decentralized setting), existing methods unfortunately remain computationally expensive due to the non-Euclidean geometry of the manifold. Our proposed algorithms, Rapid Grassmannian Averaging (RGrAv) and Decentralized Rapid Grassmannian Averaging (DRGrAv), overcome this challenge by leveraging the spectral structure of the problem to rapidly compute an average using only small matrix multiplications and QR factorizations. We provide a theoretical guarantee of optimality and present numerical experiments which demonstrate that our algorithms outperform state-of-the-art methods in providing high accuracy solutions in minimal time. Additional experiments showcase the versatility of our algorithms to tasks such as K-means clustering on video motion data, establishing RGrAv and DRGrAv as powerful tools for generic Grassmannian averaging.

MANGO: Disentangled Image Transformation Manifolds with Grouped Operators

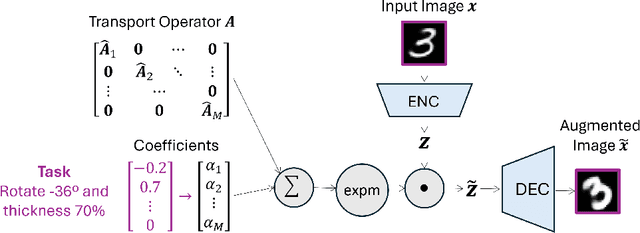
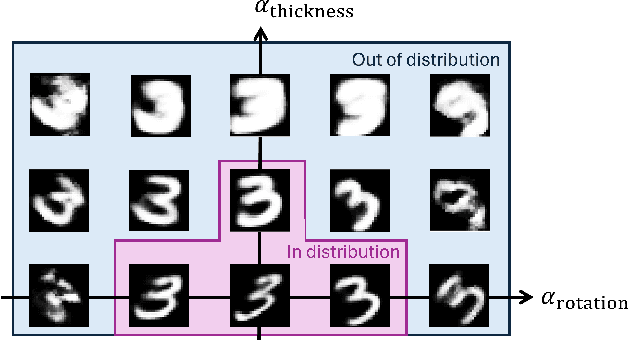
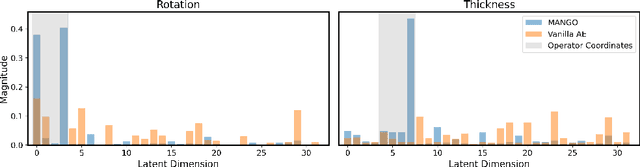
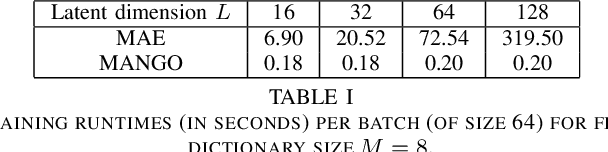
Learning semantically meaningful image transformations (i.e. rotation, thickness, blur) directly from examples can be a challenging task. Recently, the Manifold Autoencoder (MAE) proposed using a set of Lie group operators to learn image transformations directly from examples. However, this approach has limitations, as the learned operators are not guaranteed to be disentangled and the training routine is prohibitively expensive when scaling up the model. To address these limitations, we propose MANGO (transformation Manifolds with Grouped Operators) for learning disentangled operators that describe image transformations in distinct latent subspaces. Moreover, our approach allows practitioners the ability to define which transformations they aim to model, thus improving the semantic meaning of the learned operators. Through our experiments, we demonstrate that MANGO enables composition of image transformations and introduces a one-phase training routine that leads to a 100x speedup over prior works.

Subspace Tracking with Dynamical Models on the Grassmannian

Tracking signals in dynamic environments presents difficulties in both analysis and implementation. In this work, we expand on a class of subspace tracking algorithms which utilize the Grassmann manifold -- the set of linear subspaces of a high-dimensional vector space. We design regularized least squares algorithms based on common manifold operations and intuitive dynamical models. We demonstrate the efficacy of the approach for a narrowband beamforming scenario, where the dynamics of multiple signals of interest are captured by motion on the Grassmannian.

Level set methods for gradient-free optimization of metasurface arrays

Global optimization techniques are increasingly preferred over human-driven methods in the design of electromagnetic structures such as metasurfaces, and careful construction and parameterization of the physical structure is critical in ensuring computational efficiency and convergence of the optimization algorithm to a globally optimal solution. While many design variables in physical systems take discrete values, optimization algorithms often benefit from a continuous design space. This work demonstrates the use of level set functions as a continuous basis for designing material distributions for metasurface arrays and introduces an improved parameterization which is termed the periodic level set function. We explore the use of alternate norms in the definition of the level set function and define a new pseudo-inverse technique for upsampling basis coefficients with these norms. The level set method is compared to the fragmented parameterization and shows improved electromagnetic responses for two dissimilar cost functions: a narrowband objective and a broadband objective. Finally, we manufacture an optimized level set metasurface and measure its scattering parameters to demonstrate real-world performance.