Kason Ancelin
Rapid Grassmannian Averaging with Chebyshev Polynomials
Oct 11, 2024

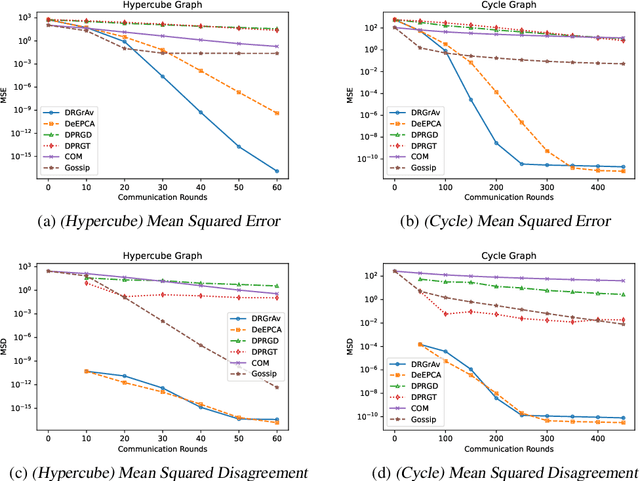

Abstract:We propose new algorithms to efficiently average a collection of points on a Grassmannian manifold in both the centralized and decentralized settings. Grassmannian points are used ubiquitously in machine learning, computer vision, and signal processing to represent data through (often low-dimensional) subspaces. While averaging these points is crucial to many tasks (especially in the decentralized setting), existing methods unfortunately remain computationally expensive due to the non-Euclidean geometry of the manifold. Our proposed algorithms, Rapid Grassmannian Averaging (RGrAv) and Decentralized Rapid Grassmannian Averaging (DRGrAv), overcome this challenge by leveraging the spectral structure of the problem to rapidly compute an average using only small matrix multiplications and QR factorizations. We provide a theoretical guarantee of optimality and present numerical experiments which demonstrate that our algorithms outperform state-of-the-art methods in providing high accuracy solutions in minimal time. Additional experiments showcase the versatility of our algorithms to tasks such as K-means clustering on video motion data, establishing RGrAv and DRGrAv as powerful tools for generic Grassmannian averaging.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge