Global Convergence of Adaptive Sensing for Principal Eigenvector Estimation

This paper addresses the challenge of efficient principal component analysis (PCA) in high-dimensional spaces by analyzing a compressively sampled variant of Oja's algorithm with adaptive sensing. Traditional PCA methods incur substantial computational costs that scale poorly with data dimensionality, whereas subspace tracking algorithms like Oja's offer more efficient alternatives but typically require full-dimensional observations. We analyze a variant where, at each iteration, only two compressed measurements are taken: one in the direction of the current estimate and one in a random orthogonal direction. We prove that this adaptive sensing approach achieves global convergence in the presence of noise when tracking the leading eigenvector of a datastream with eigengap $\Delta=\lambda_1-\lambda_2$. Our theoretical analysis demonstrates that the algorithm experiences two phases: (1) a warmup phase requiring $O(\lambda_1\lambda_2d^2/\Delta^2)$ iterations to achieve a constant-level alignment with the true eigenvector, followed by (2) a local convergence phase where the sine alignment error decays at a rate of $O(\lambda_1\lambda_2d^2/\Delta^2 t)$ for iterations $t$. The guarantee aligns with existing minimax lower bounds with an added factor of $d$ due to the compressive sampling. This work provides the first convergence guarantees in adaptive sensing for subspace tracking with noise. Our proof technique is also considerably simpler than those in prior works. The results have important implications for applications where acquiring full-dimensional samples is challenging or costly.

Rapid Grassmannian Averaging with Chebyshev Polynomials

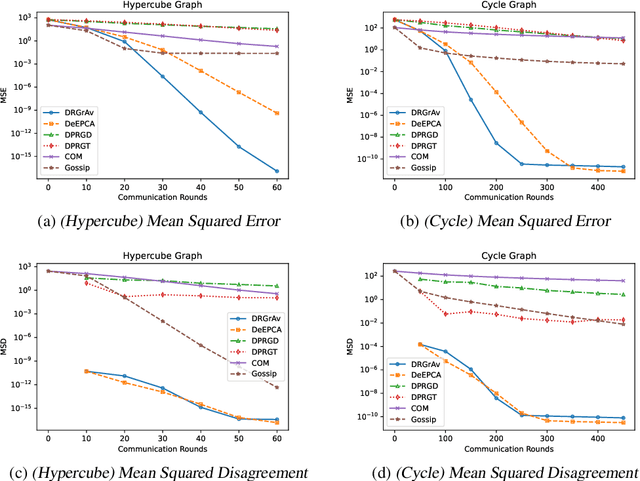
We propose new algorithms to efficiently average a collection of points on a Grassmannian manifold in both the centralized and decentralized settings. Grassmannian points are used ubiquitously in machine learning, computer vision, and signal processing to represent data through (often low-dimensional) subspaces. While averaging these points is crucial to many tasks (especially in the decentralized setting), existing methods unfortunately remain computationally expensive due to the non-Euclidean geometry of the manifold. Our proposed algorithms, Rapid Grassmannian Averaging (RGrAv) and Decentralized Rapid Grassmannian Averaging (DRGrAv), overcome this challenge by leveraging the spectral structure of the problem to rapidly compute an average using only small matrix multiplications and QR factorizations. We provide a theoretical guarantee of optimality and present numerical experiments which demonstrate that our algorithms outperform state-of-the-art methods in providing high accuracy solutions in minimal time. Additional experiments showcase the versatility of our algorithms to tasks such as K-means clustering on video motion data, establishing RGrAv and DRGrAv as powerful tools for generic Grassmannian averaging.

MANGO: Disentangled Image Transformation Manifolds with Grouped Operators

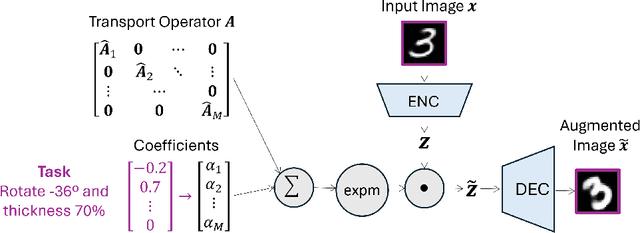
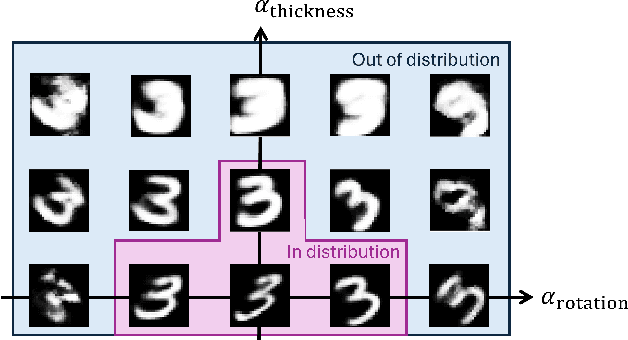
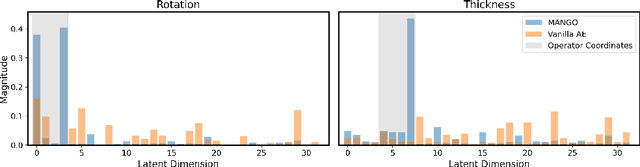
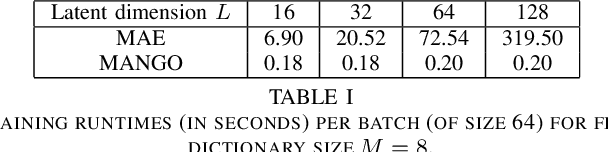
Learning semantically meaningful image transformations (i.e. rotation, thickness, blur) directly from examples can be a challenging task. Recently, the Manifold Autoencoder (MAE) proposed using a set of Lie group operators to learn image transformations directly from examples. However, this approach has limitations, as the learned operators are not guaranteed to be disentangled and the training routine is prohibitively expensive when scaling up the model. To address these limitations, we propose MANGO (transformation Manifolds with Grouped Operators) for learning disentangled operators that describe image transformations in distinct latent subspaces. Moreover, our approach allows practitioners the ability to define which transformations they aim to model, thus improving the semantic meaning of the learned operators. Through our experiments, we demonstrate that MANGO enables composition of image transformations and introduces a one-phase training routine that leads to a 100x speedup over prior works.

Subspace Tracking with Dynamical Models on the Grassmannian

Tracking signals in dynamic environments presents difficulties in both analysis and implementation. In this work, we expand on a class of subspace tracking algorithms which utilize the Grassmann manifold -- the set of linear subspaces of a high-dimensional vector space. We design regularized least squares algorithms based on common manifold operations and intuitive dynamical models. We demonstrate the efficacy of the approach for a narrowband beamforming scenario, where the dynamics of multiple signals of interest are captured by motion on the Grassmannian.

Decentralized Feature-Distributed Optimization for Generalized Linear Models

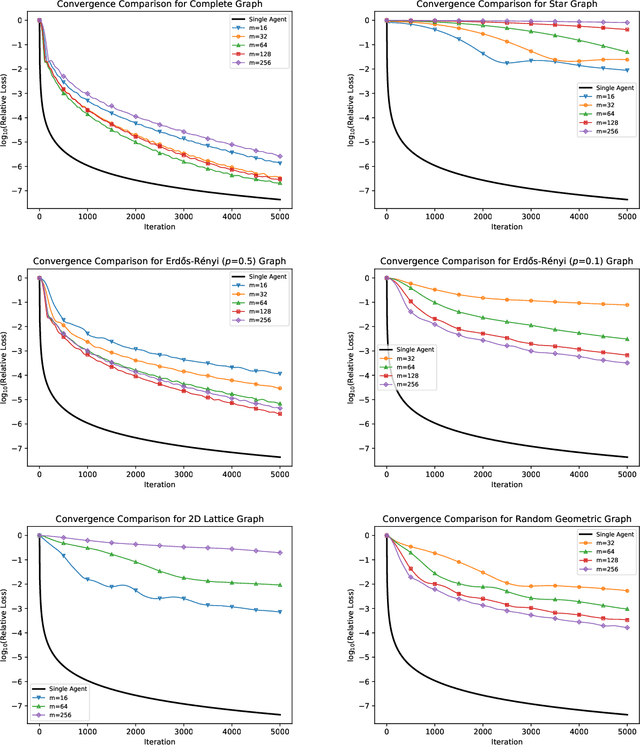
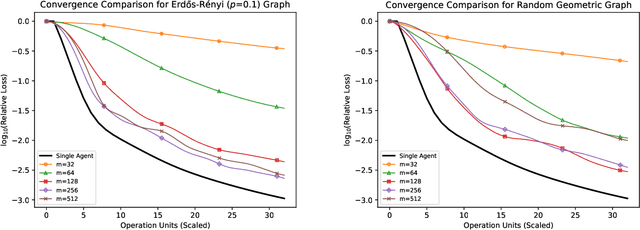
We consider the "all-for-one" decentralized learning problem for generalized linear models. The features of each sample are partitioned among several collaborating agents in a connected network, but only one agent observes the response variables. To solve the regularized empirical risk minimization in this distributed setting, we apply the Chambolle--Pock primal--dual algorithm to an equivalent saddle-point formulation of the problem. The primal and dual iterations are either in closed-form or reduce to coordinate-wise minimization of scalar convex functions. We establish convergence rates for the empirical risk minimization under two different assumptions on the loss function (Lipschitz and square root Lipschitz), and show how they depend on the characteristics of the design matrix and the Laplacian of the network.