MANGO: Disentangled Image Transformation Manifolds with Grouped Operators

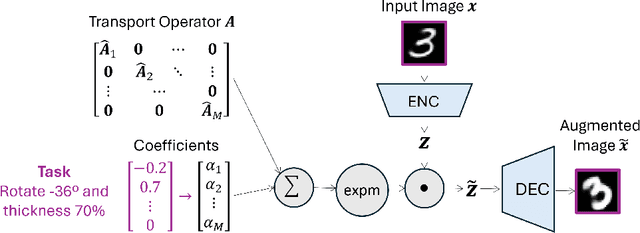
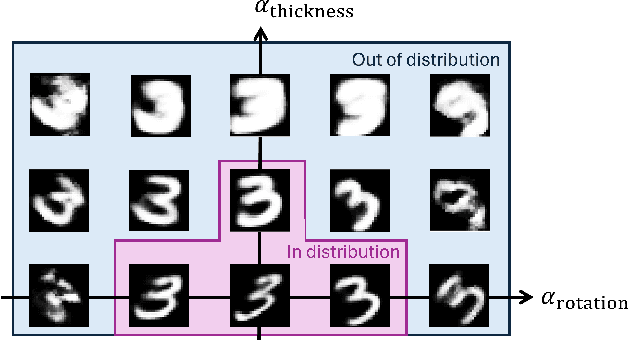
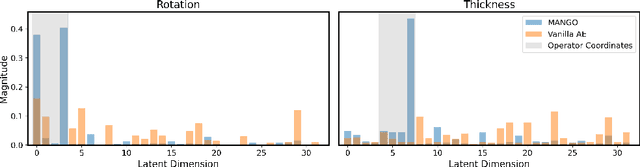
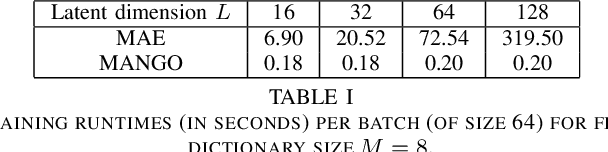
Learning semantically meaningful image transformations (i.e. rotation, thickness, blur) directly from examples can be a challenging task. Recently, the Manifold Autoencoder (MAE) proposed using a set of Lie group operators to learn image transformations directly from examples. However, this approach has limitations, as the learned operators are not guaranteed to be disentangled and the training routine is prohibitively expensive when scaling up the model. To address these limitations, we propose MANGO (transformation Manifolds with Grouped Operators) for learning disentangled operators that describe image transformations in distinct latent subspaces. Moreover, our approach allows practitioners the ability to define which transformations they aim to model, thus improving the semantic meaning of the learned operators. Through our experiments, we demonstrate that MANGO enables composition of image transformations and introduces a one-phase training routine that leads to a 100x speedup over prior works.

Robust Broadband Beamforming using Bilinear Programming

We introduce a new method for robust beamforming, where the goal is to estimate a signal from array samples when there is uncertainty in the angle of arrival. Our method offers state-of-the-art performance on narrowband signals and is naturally applied to broadband signals. Our beamformer operates by treating the forward model for the array samples as unknown. We show that the "true" forward model lies in the linear span of a small number of fixed linear systems. As a result, we can estimate the forward operator and the signal simultaneously by solving a bilinear inverse problem using least squares. Our numerical experiments show that if the angle of arrival is known to only be within an interval of reasonable size, there is very little loss in estimation performance compared to the case where the angle is known exactly.