Decentralized Feature-Distributed Optimization for Generalized Linear Models
Paper and Code
Oct 28, 2021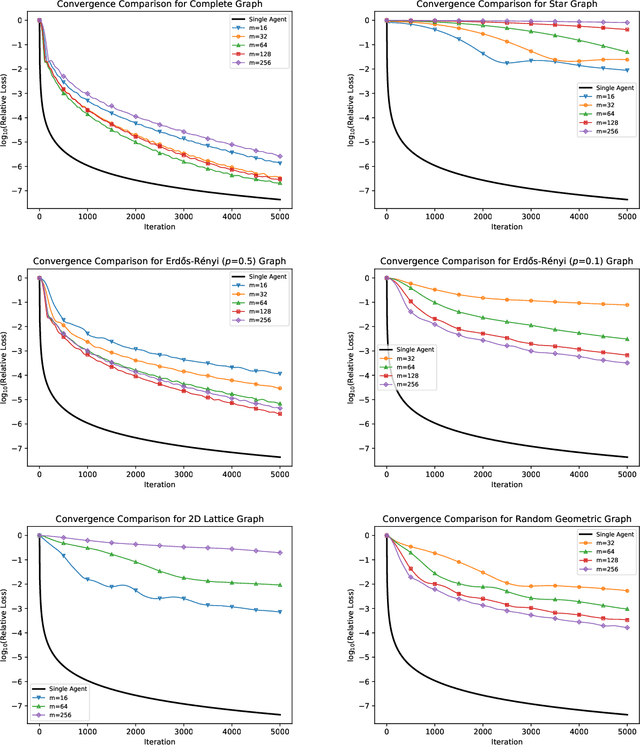
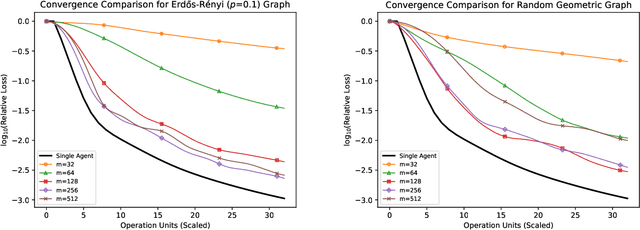
We consider the "all-for-one" decentralized learning problem for generalized linear models. The features of each sample are partitioned among several collaborating agents in a connected network, but only one agent observes the response variables. To solve the regularized empirical risk minimization in this distributed setting, we apply the Chambolle--Pock primal--dual algorithm to an equivalent saddle-point formulation of the problem. The primal and dual iterations are either in closed-form or reduce to coordinate-wise minimization of scalar convex functions. We establish convergence rates for the empirical risk minimization under two different assumptions on the loss function (Lipschitz and square root Lipschitz), and show how they depend on the characteristics of the design matrix and the Laplacian of the network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge