A Fundamental Accuracy--Robustness Trade-off in Regression and Classification

We derive a fundamental trade-off between standard and adversarial risk in a rather general situation that formalizes the following simple intuition: "If no (nearly) optimal predictor is smooth, adversarial robustness comes at the cost of accuracy." As a concrete example, we evaluate the derived trade-off in regression with polynomial ridge functions under mild regularity conditions.

Instance-dependent uniform tail bounds for empirical processes

We formulate a uniform tail bound for empirical processes indexed by a class of functions, in terms of the individual deviations of the functions rather than the worst-case deviation in the considered class. The tail bound is established by introducing an initial "deflation" step to the standard generic chaining argument. The resulting tail bound has a main complexity component, a variant of Talagrand's $\gamma$ functional for the deflated function class, as well as an instance-dependent deviation term, measured by an appropriately scaled version of a suitable norm. Both of these terms are expressed using certain coefficients formulated based on the relevant cumulant generating functions. We also provide more explicit approximations for the mentioned coefficients, when the function class lies in a given (exponential type) Orlicz space.

Decentralized Feature-Distributed Optimization for Generalized Linear Models

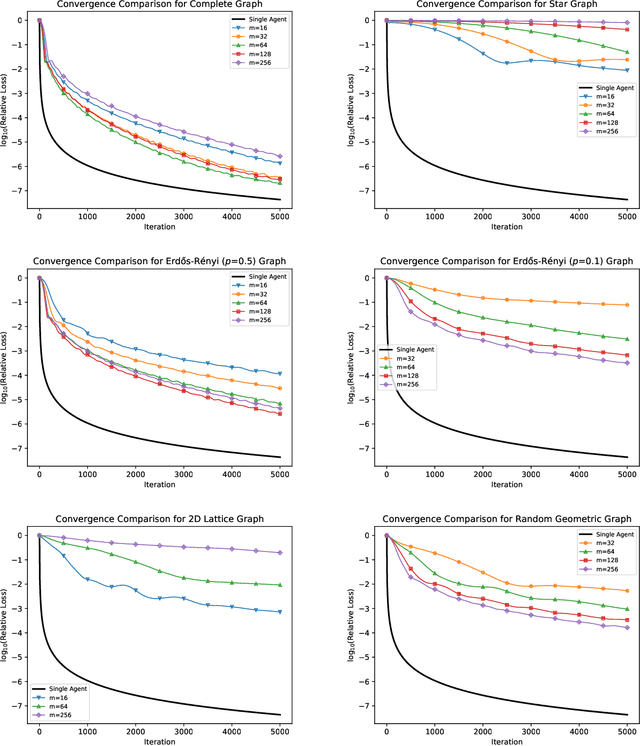
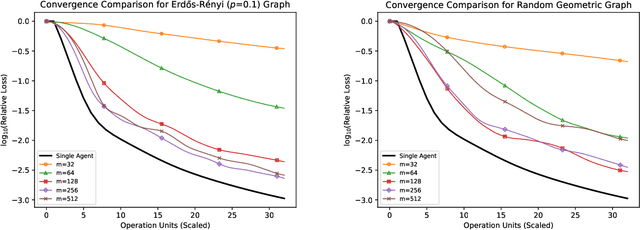
We consider the "all-for-one" decentralized learning problem for generalized linear models. The features of each sample are partitioned among several collaborating agents in a connected network, but only one agent observes the response variables. To solve the regularized empirical risk minimization in this distributed setting, we apply the Chambolle--Pock primal--dual algorithm to an equivalent saddle-point formulation of the problem. The primal and dual iterations are either in closed-form or reduce to coordinate-wise minimization of scalar convex functions. We establish convergence rates for the empirical risk minimization under two different assumptions on the loss function (Lipschitz and square root Lipschitz), and show how they depend on the characteristics of the design matrix and the Laplacian of the network.

Max-Linear Regression by Scalable and Guaranteed Convex Programming

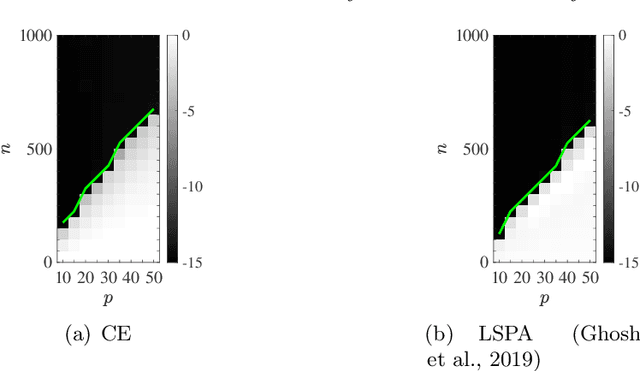
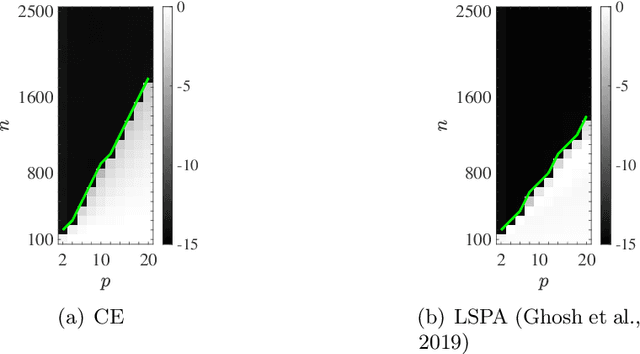
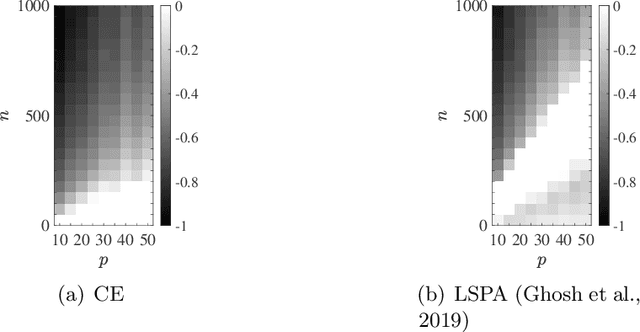
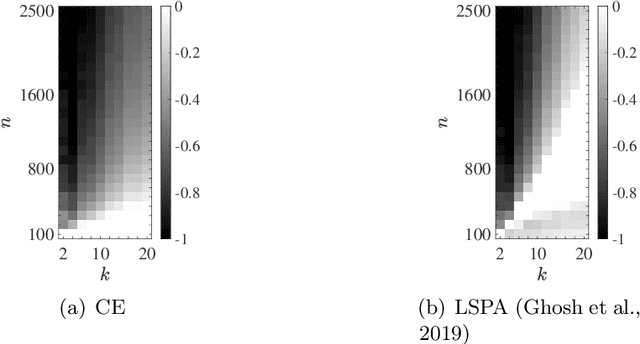
We consider the multivariate max-linear regression problem where the model parameters $\boldsymbol{\beta}_{1},\dotsc,\boldsymbol{\beta}_{k}\in\mathbb{R}^{p}$ need to be estimated from $n$ independent samples of the (noisy) observations $y = \max_{1\leq j \leq k} \boldsymbol{\beta}_{j}^{\mathsf{T}} \boldsymbol{x} + \mathrm{noise}$. The max-linear model vastly generalizes the conventional linear model, and it can approximate any convex function to an arbitrary accuracy when the number of linear models $k$ is large enough. However, the inherent nonlinearity of the max-linear model renders the estimation of the regression parameters computationally challenging. Particularly, no estimator based on convex programming is known in the literature. We formulate and analyze a scalable convex program as the estimator for the max-linear regression problem. Under the standard Gaussian observation setting, we present a non-asymptotic performance guarantee showing that the convex program recovers the parameters with high probability. When the $k$ linear components are equally likely to achieve the maximum, our result shows that a sufficient number of observations scales as $k^{2}p$ up to a logarithmic factor. This significantly improves on the analogous prior result based on alternating minimization (Ghosh et al., 2019). Finally, through a set of Monte Carlo simulations, we illustrate that our theoretical result is consistent with empirical behavior, and the convex estimator for max-linear regression is as competitive as the alternating minimization algorithm in practice.

Low-Rank Matrix Estimation From Rank-One Projections by Unlifted Convex Optimization

We study an estimator with a convex formulation for recovery of low-rank matrices from rank-one projections. Using initial estimates of the factors of the target $d_1\times d_2$ matrix of rank-$r$, the estimator operates as a standard quadratic program in a space of dimension $r(d_1+d_2)$. This property makes the estimator significantly more scalable than the convex estimators based on lifting and semidefinite programming. Furthermore, we present a streamlined analysis for exact recovery under the real Gaussian measurement model, as well as the partially derandomized measurement model by using the spherical 2-design. We show that under both models the estimator succeeds, with high probability, if the number of measurements exceeds $r^2 (d_1+d_2)$ up to some logarithmic factors. This sample complexity improves on the existing results for nonconvex iterative algorithms.

Convex Programming for Estimation in Nonlinear Recurrent Models

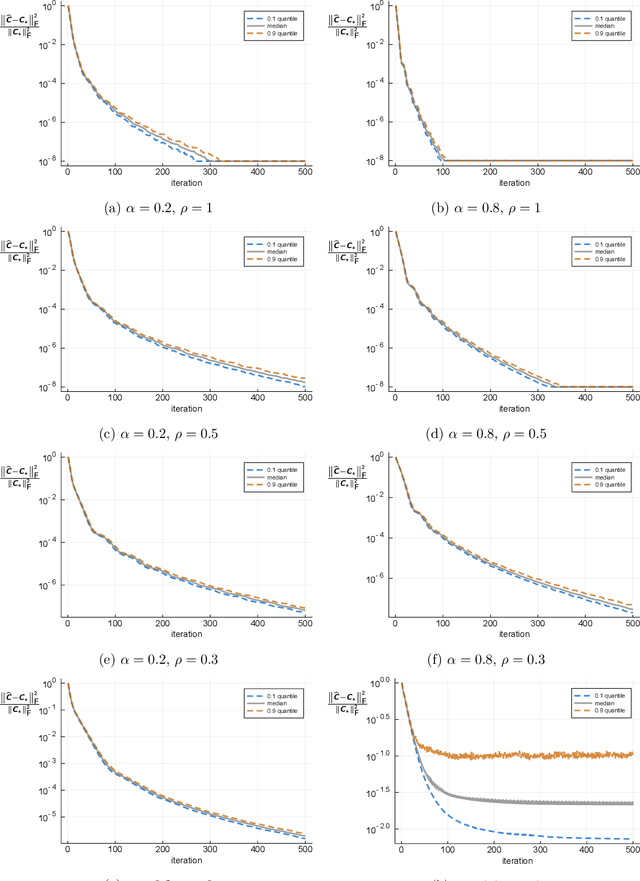
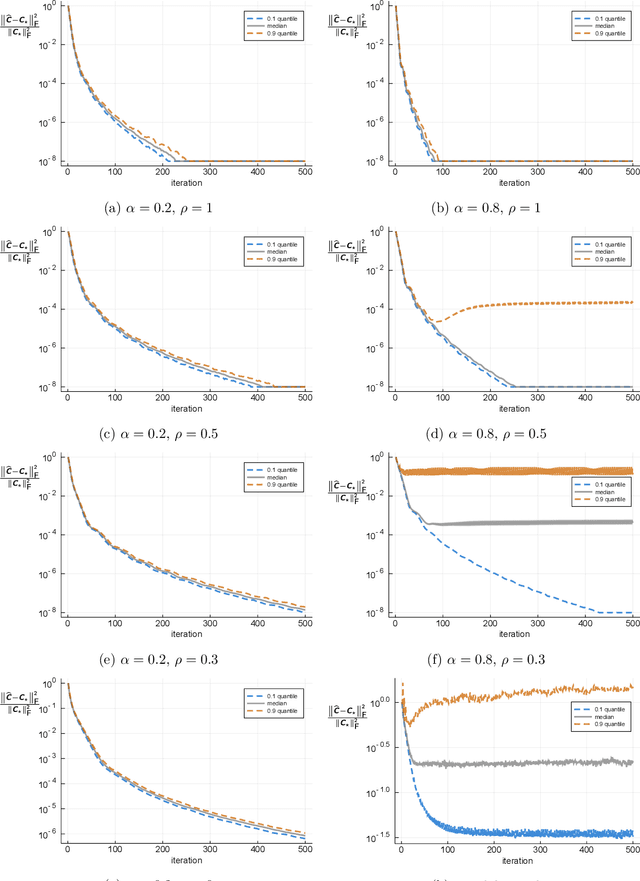
We propose a formulation for nonlinear recurrent models that includes simple parametric models of recurrent neural networks as a special case. The proposed formulation leads to a natural estimator in the form of a convex program. We provide a sample complexity for this estimator in the case of stable dynamics, where the nonlinear recursion has a certain contraction property, and under certain regularity conditions on the input distribution. We evaluate the performance of the estimator by simulation on synthetic data. These numerical experiments also suggest the extent at which the imposed theoretical assumptions may be relaxed.

Solving Equations of Random Convex Functions via Anchored Regression

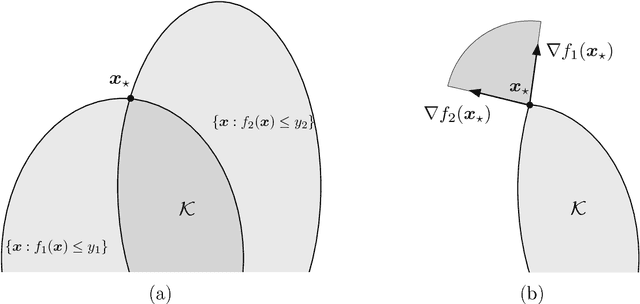
We consider the question of estimating a solution to a system of equations that involve convex nonlinearities, a problem that is common in machine learning and signal processing. Because of these nonlinearities, conventional estimators based on empirical risk minimization generally involve solving a non-convex optimization program. We propose anchored regression, a new approach based on convex programming that amounts to maximizing a linear functional (perhaps augmented by a regularizer) over a convex set. The proposed convex program is formulated in the natural space of the problem, and avoids the introduction of auxiliary variables, making it computationally favorable. Working in the native space also provides great flexibility as structural priors (e.g., sparsity) can be seamlessly incorporated. For our analysis, we model the equations as being drawn from a fixed set according to a probability law. Our main results provide guarantees on the accuracy of the estimator in terms of the number of equations we are solving, the amount of noise present, a measure of statistical complexity of the random equations, and the geometry of the regularizer at the true solution. We also provide recipes for constructing the anchor vector (that determines the linear functional to maximize) directly from the observed data.

Estimation from Non-Linear Observations via Convex Programming with Application to Bilinear Regression

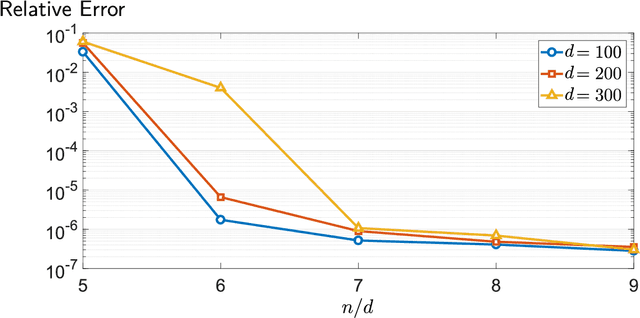
We propose a computationally efficient estimator, formulated as a convex program, for a broad class of non-linear regression problems that involve difference of convex (DC) non-linearities. The proposed method can be viewed as a significant extension of the "anchored regression" method formulated and analyzed in [9] for regression with convex non-linearities. Our main assumption, in addition to other mild statistical and computational assumptions, is availability of a certain approximation oracle for the average of the gradients of the observation functions at a ground truth. Under this assumption and using a PAC-Bayesian analysis we show that the proposed estimator produces an accurate estimate with high probability. As a concrete example, we study the proposed framework in the bilinear regression problem with Gaussian factors and quantify a sufficient sample complexity for exact recovery. Furthermore, we describe a computationally tractable scheme that provably produces the required approximation oracle in the considered bilinear regression problem.

Phase Retrieval Meets Statistical Learning Theory: A Flexible Convex Relaxation

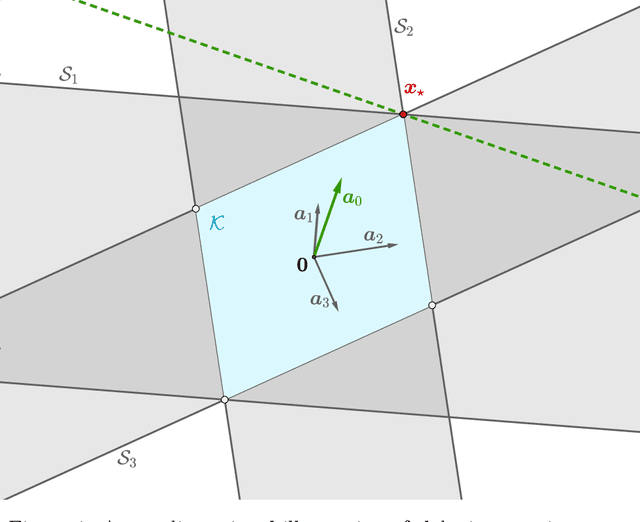
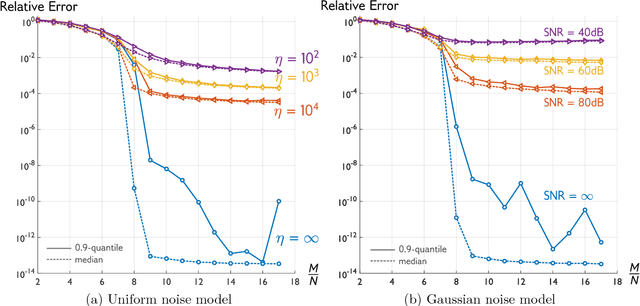
We propose a flexible convex relaxation for the phase retrieval problem that operates in the natural domain of the signal. Therefore, we avoid the prohibitive computational cost associated with "lifting" and semidefinite programming (SDP) in methods such as PhaseLift and compete with recently developed non-convex techniques for phase retrieval. We relax the quadratic equations for phaseless measurements to inequality constraints each of which representing a symmetric "slab". Through a simple convex program, our proposed estimator finds an extreme point of the intersection of these slabs that is best aligned with a given anchor vector. We characterize geometric conditions that certify success of the proposed estimator. Furthermore, using classic results in statistical learning theory, we show that for random measurements the geometric certificates hold with high probability at an optimal sample complexity. Phase transition of our estimator is evaluated through simulations. Our numerical experiments also suggest that the proposed method can solve phase retrieval problems with coded diffraction measurements as well.

Learning Model-Based Sparsity via Projected Gradient Descent

Several convex formulation methods have been proposed previously for statistical estimation with structured sparsity as the prior. These methods often require a carefully tuned regularization parameter, often a cumbersome or heuristic exercise. Furthermore, the estimate that these methods produce might not belong to the desired sparsity model, albeit accurately approximating the true parameter. Therefore, greedy-type algorithms could often be more desirable in estimating structured-sparse parameters. So far, these greedy methods have mostly focused on linear statistical models. In this paper we study the projected gradient descent with non-convex structured-sparse parameter model as the constraint set. Should the cost function have a Stable Model-Restricted Hessian the algorithm produces an approximation for the desired minimizer. As an example we elaborate on application of the main results to estimation in Generalized Linear Model.