Variable Selection in Convex Piecewise Linear Regression

This paper presents Sparse Gradient Descent as a solution for variable selection in convex piecewise linear regression where the model is given as $\mathrm{max}\langle a_j^\star, x \rangle + b_j^\star$ for $j = 1,\dots,k$ where $x \in \mathbb R^d$ is the covariate vector. Here, $\{a_j^\star\}_{j=1}^k$ and $\{b_j^\star\}_{j=1}^k$ denote the ground-truth weight vectors and intercepts. A non-asymptotic local convergence analysis is provided for Sp-GD under sub-Gaussian noise when the covariate distribution satisfies sub-Gaussianity and anti-concentration property. When the model order and parameters are fixed, Sp-GD provides an $\epsilon$-accurate estimate given $\mathcal{O}(\max(\epsilon^{-2}\sigma_z^2,1)s\log(d/s))$ observations where $\sigma_z^2$ denotes the noise variance. This also implies the exact parameter recovery by Sp-GD from $\mathcal{O}(s\log(d/s))$ noise-free observations. Since optimizing the squared loss for sparse max-affine is non-convex, an initialization scheme is proposed to provide a suitable initial estimate within the basin of attraction for Sp-GD, i.e. sufficiently accurate to invoke the convergence guarantees. The initialization scheme uses sparse principal component analysis to estimate the subspace spanned by $\{ a_j^\star\}_{j=1}^k$ then applies an $r$-covering search to estimate the model parameters. A non-asymptotic analysis is presented for this initialization scheme when the covariates and noise samples follow Gaussian distributions. When the model order and parameters are fixed, this initialization scheme provides an $\epsilon$-accurate estimate given $\mathcal{O}(\epsilon^{-2}\max(\sigma_z^4,\sigma_z^2,1)s^2\log^4(d))$ observations. Numerical Monte Carlo results corroborate theoretical findings for Sp-GD and the initialization scheme.

Small-Noise Sensitivity Analysis of Locating Pulses in the Presence of Adversarial Perturbation

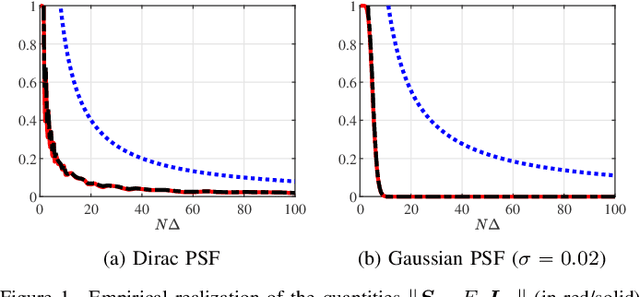
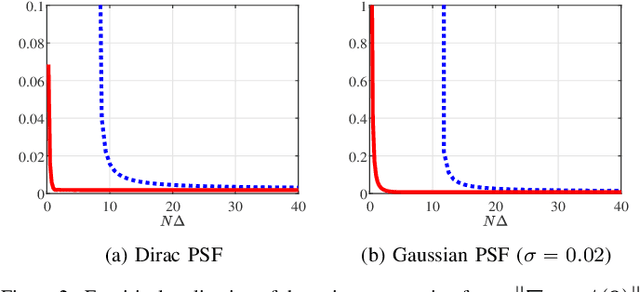
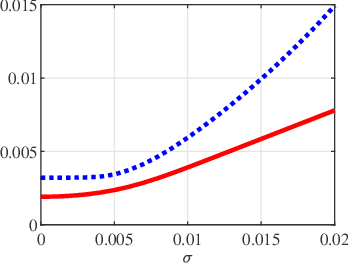
A fundamental small-noise sensitivity analysis of spike localization in the presence of adversarial perturbations and arbitrary point spread function (PSF) is presented. The analysis leverages the local Lipschitz property of the inverse map from measurement noise to parameter estimate. In the small noise regime, the local Lipschitz constant converges to the spectral norm of the noiseless Jacobian of the inverse map. An interpretable upper bound in terms of the minimum separation of spikes, norms, and flatness of the PSF and its derivative, and the distribution of spike amplitudes is provided. Numerical experiments highlighting the relevance of the theoretical bound as a proxy to the local Lipschitz constant and its dependence on the key attributes of the problem are presented.

Stable estimation of pulses of unknown shape from multiple snapshots via ESPRIT

We consider the problem of resolving overlapping pulses from noisy multi-snapshot measurements, which has been a problem central to various applications including medical imaging and array signal processing. ESPRIT algorithm has been used to estimate the pulse locations. However, existing theoretical analysis is restricted to ideal assumptions on signal and measurement models. We present a novel perturbation analysis that overcomes the previous theoretical limitation, which is derived without a stringent assumption on the signal model. Our unifying analysis applies to various sub-array designs of the ESPRIT algorithm. We demonstrate the usefulness of the perturbation analysis by specifying the result in two practical scenarios. In the first scenario, we quantify how the number of snapshots for stable recovery scales when the number of Fourier measurements per snapshot is sufficiently large. In the second scenario, we propose compressive blind array calibration by ESPRIT with random sub-arrays and provide the corresponding non-asymptotic error bound. Furthermore, we demonstrate that the empirical performance of ESPRIT corroborates the theoretical analysis through extensive numerical results.

Max-affine regression via first-order methods

We consider regression of a max-affine model that produces a piecewise linear model by combining affine models via the max function. The max-affine model ubiquitously arises in applications in signal processing and statistics including multiclass classification, auction problems, and convex regression. It also generalizes phase retrieval and learning rectifier linear unit activation functions. We present a non-asymptotic convergence analysis of gradient descent (GD) and mini-batch stochastic gradient descent (SGD) for max-affine regression when the model is observed at random locations following the sub-Gaussianity and an anti-concentration with additive sub-Gaussian noise. Under these assumptions, a suitably initialized GD and SGD converge linearly to a neighborhood of the ground truth specified by the corresponding error bound. We provide numerical results that corroborate the theoretical finding. Importantly, SGD not only converges faster in run time with fewer observations than alternating minimization and GD in the noiseless scenario but also outperforms them in low-sample scenarios with noise.

Randomly Initialized Alternating Least Squares: Fast Convergence for Matrix Sensing

We consider the problem of reconstructing rank-one matrices from random linear measurements, a task that appears in a variety of problems in signal processing, statistics, and machine learning. In this paper, we focus on the Alternating Least Squares (ALS) method. While this algorithm has been studied in a number of previous works, most of them only show convergence from an initialization close to the true solution and thus require a carefully designed initialization scheme. However, random initialization has often been preferred by practitioners as it is model-agnostic. In this paper, we show that ALS with random initialization converges to the true solution with $\varepsilon$-accuracy in $O(\log n + \log (1/\varepsilon)) $ iterations using only a near-optimal amount of samples, where we assume the measurement matrices to be i.i.d. Gaussian and where by $n$ we denote the ambient dimension. Key to our proof is the observation that the trajectory of the ALS iterates only depends very mildly on certain entries of the random measurement matrices. Numerical experiments corroborate our theoretical predictions.

Max-Linear Regression by Scalable and Guaranteed Convex Programming

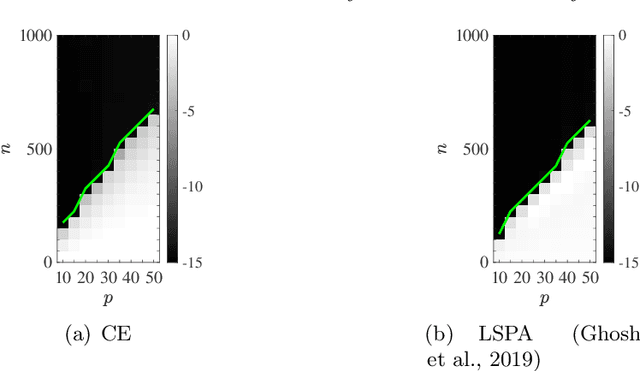
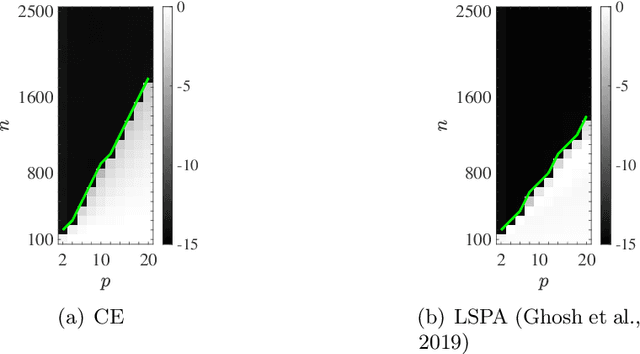
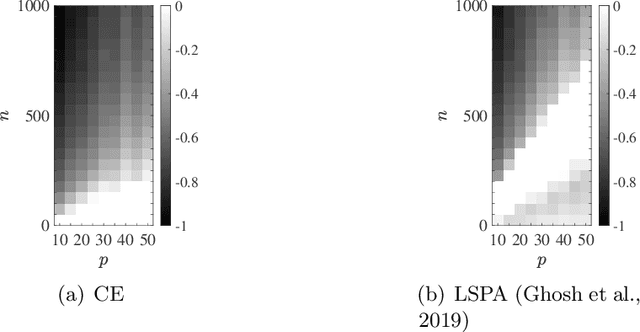
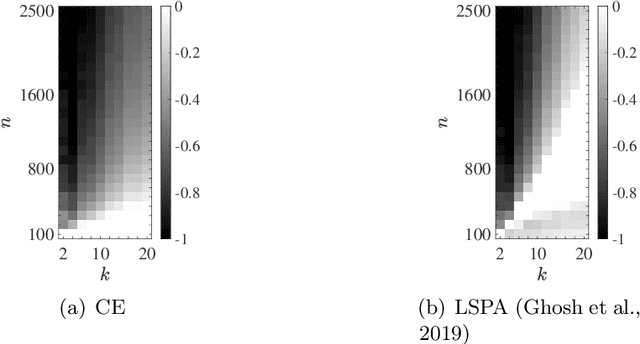
We consider the multivariate max-linear regression problem where the model parameters $\boldsymbol{\beta}_{1},\dotsc,\boldsymbol{\beta}_{k}\in\mathbb{R}^{p}$ need to be estimated from $n$ independent samples of the (noisy) observations $y = \max_{1\leq j \leq k} \boldsymbol{\beta}_{j}^{\mathsf{T}} \boldsymbol{x} + \mathrm{noise}$. The max-linear model vastly generalizes the conventional linear model, and it can approximate any convex function to an arbitrary accuracy when the number of linear models $k$ is large enough. However, the inherent nonlinearity of the max-linear model renders the estimation of the regression parameters computationally challenging. Particularly, no estimator based on convex programming is known in the literature. We formulate and analyze a scalable convex program as the estimator for the max-linear regression problem. Under the standard Gaussian observation setting, we present a non-asymptotic performance guarantee showing that the convex program recovers the parameters with high probability. When the $k$ linear components are equally likely to achieve the maximum, our result shows that a sufficient number of observations scales as $k^{2}p$ up to a logarithmic factor. This significantly improves on the analogous prior result based on alternating minimization (Ghosh et al., 2019). Finally, through a set of Monte Carlo simulations, we illustrate that our theoretical result is consistent with empirical behavior, and the convex estimator for max-linear regression is as competitive as the alternating minimization algorithm in practice.

Low-Rank Matrix Estimation From Rank-One Projections by Unlifted Convex Optimization

We study an estimator with a convex formulation for recovery of low-rank matrices from rank-one projections. Using initial estimates of the factors of the target $d_1\times d_2$ matrix of rank-$r$, the estimator operates as a standard quadratic program in a space of dimension $r(d_1+d_2)$. This property makes the estimator significantly more scalable than the convex estimators based on lifting and semidefinite programming. Furthermore, we present a streamlined analysis for exact recovery under the real Gaussian measurement model, as well as the partially derandomized measurement model by using the spherical 2-design. We show that under both models the estimator succeeds, with high probability, if the number of measurements exceeds $r^2 (d_1+d_2)$ up to some logarithmic factors. This sample complexity improves on the existing results for nonconvex iterative algorithms.

Blind Gain and Phase Calibration via Sparse Spectral Methods

Blind gain and phase calibration (BGPC) is a bilinear inverse problem involving the determination of unknown gains and phases of the sensing system, and the unknown signal, jointly. BGPC arises in numerous applications, e.g., blind albedo estimation in inverse rendering, synthetic aperture radar autofocus, and sensor array auto-calibration. In some cases, sparse structure in the unknown signal alleviates the ill-posedness of BGPC. Recently there has been renewed interest in solutions to BGPC with careful analysis of error bounds. In this paper, we formulate BGPC as an eigenvalue/eigenvector problem, and propose to solve it via power iteration, or in the sparsity or joint sparsity case, via truncated power iteration. Under certain assumptions, the unknown gains, phases, and the unknown signal can be recovered simultaneously. Numerical experiments show that power iteration algorithms work not only in the regime predicted by our main results, but also in regimes where theoretical analysis is limited. We also show that our power iteration algorithms for BGPC compare favorably with competing algorithms in adversarial conditions, e.g., with noisy measurement or with a bad initial estimate.

Generalized notions of sparsity and restricted isometry property. Part II: Applications

The restricted isometry property (RIP) is a universal tool for data recovery. We explore the implication of the RIP in the framework of generalized sparsity and group measurements introduced in the Part I paper. It turns out that for a given measurement instrument the number of measurements for RIP can be improved by optimizing over families of Banach spaces. Second, we investigate the preservation of difference of two sparse vectors, which is not trivial in generalized models. Third, we extend the RIP of partial Fourier measurements at optimal scaling of number of measurements with random sign to far more general group structured measurements. Lastly, we also obtain RIP in infinite dimension in the context of Fourier measurement concepts with sparsity naturally replaced by smoothness assumptions.

Generalized notions of sparsity and restricted isometry property. Part I: A unified framework

The restricted isometry property (RIP) is an integral tool in the analysis of various inverse problems with sparsity models. Motivated by the applications of compressed sensing and dimensionality reduction of low-rank tensors, we propose generalized notions of sparsity and provide a unified framework for the corresponding RIP, in particular when combined with isotropic group actions. Our results extend an approach by Rudelson and Vershynin to a much broader context including commutative and noncommutative function spaces. Moreover, our Banach space notion of sparsity applies to affine group actions. The generalized approach in particular applies to high order tensor products.