Small-Noise Sensitivity Analysis of Locating Pulses in the Presence of Adversarial Perturbation

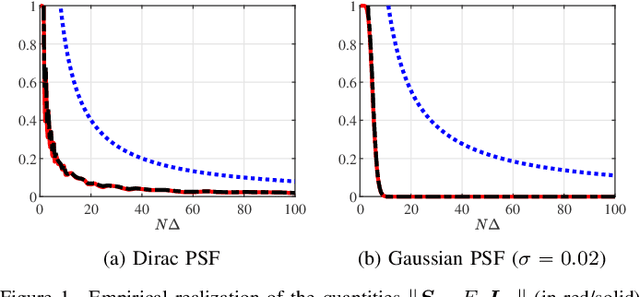
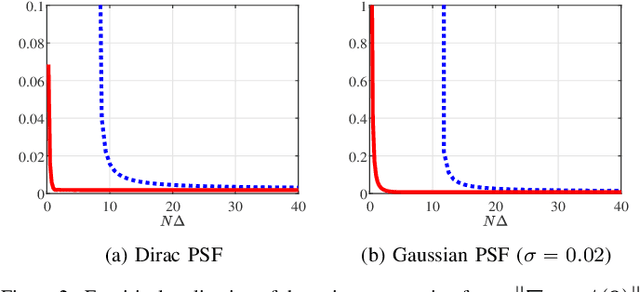
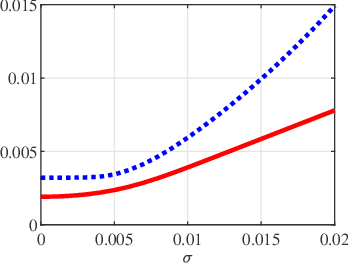
A fundamental small-noise sensitivity analysis of spike localization in the presence of adversarial perturbations and arbitrary point spread function (PSF) is presented. The analysis leverages the local Lipschitz property of the inverse map from measurement noise to parameter estimate. In the small noise regime, the local Lipschitz constant converges to the spectral norm of the noiseless Jacobian of the inverse map. An interpretable upper bound in terms of the minimum separation of spikes, norms, and flatness of the PSF and its derivative, and the distribution of spike amplitudes is provided. Numerical experiments highlighting the relevance of the theoretical bound as a proxy to the local Lipschitz constant and its dependence on the key attributes of the problem are presented.

Physical Layer Location Privacy in SIMO Communication Using Fake Paths Injection

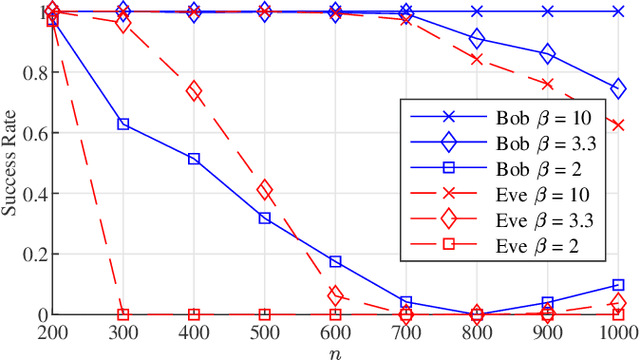
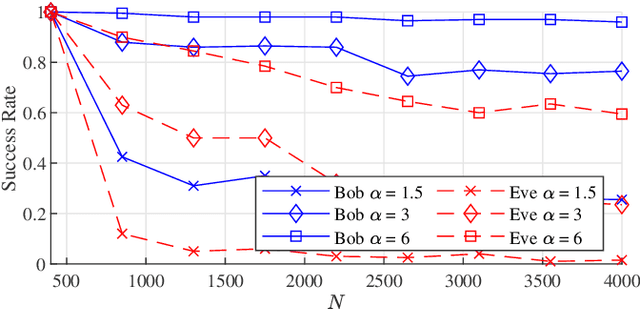
Fake path injection is an emerging paradigm for inducing privacy over wireless networks. In this paper, fake paths are injected by the transmitter into a SIMO multipath communication channel to preserve her physical location from an eavesdropper. A novel statistical privacy metric is defined as the ratio between the largest (resp. smallest) eigenvalues of Bob's (resp. Eve's) Cram\'er-Rao lower bound on the SIMO multipath channel parameters to assess the privacy enhancements. Leveraging the spectral properties of generalized Vandermonde matrices, bounds on the privacy margin of the proposed scheme are derived. Specifically, it is shown that the privacy margin increases quadratically in the inverse of the separation between the true and the fake paths under Eve's perspective. Numerical simulations further showcase the approach's benefit.

Guaranteed Private Communication with Secret Block Structure

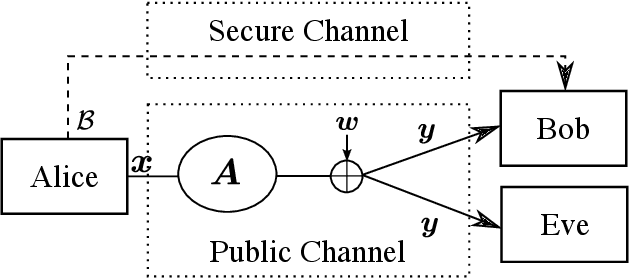
A novel private communication framework is proposed where privacy is induced by transmitting over channel instances of linear inverse problems that are identifiable to the legitimate receiver, but unidentifiable to an eavesdropper. The gap in identifiability is created in the framework by leveraging secret knowledge between the transmitter and the legitimate receiver. Specifically, the case where the legitimate receiver harnesses a secret block structure to decode a transmitted block-sparse message from underdetermined linear measurements in conditions where classical compressed sensing would provably fail is examined. The applicability of the proposed scheme to practical multiple access wireless communication systems is discussed. The protocol's privacy is studied under a single transmission, and under multiple transmissions without refreshing the secret block structure. It is shown that, under a specific scaling of the channel dimensions and transmission parameters, the eavesdropper can attempt to overhear the block structure from the fourth-order moments of the channel output. Computation of a statistical lower bound, suggests that the proposed fourth-order moment secret block estimation strategy is near optimal. The performance of a spectral clustering algorithm is studied to that end, defining scaling laws on the lifespan of the secret key before the communication is compromised. Finally, numerical experiments corroborating the theoretical findings are conducted.

Local Geometry of Nonconvex Spike Deconvolution from Low-Pass Measurements

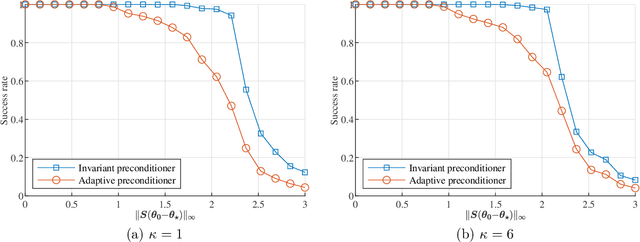
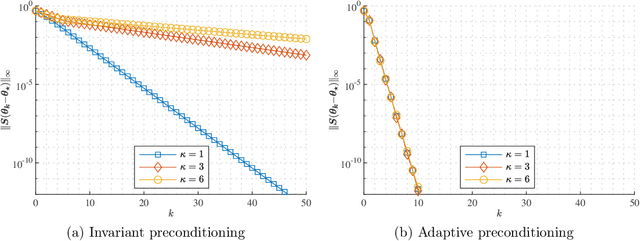
Spike deconvolution is the problem of recovering the point sources from their convolution with a known point spread function, which plays a fundamental role in many sensing and imaging applications. In this paper, we investigate the local geometry of recovering the parameters of point sources$\unicode{x2014}$including both amplitudes and locations$\unicode{x2014}$by minimizing a natural nonconvex least-squares loss function measuring the observation residuals. We propose preconditioned variants of gradient descent (GD), where the search direction is scaled via some carefully designed preconditioning matrices. We begin with a simple fixed preconditioner design, which adjusts the learning rates of the locations at a different scale from those of the amplitudes, and show it achieves a linear rate of convergence$\unicode{x2014}$in terms of entrywise errors$\unicode{x2014}$when initialized close to the ground truth, as long as the separation between the true spikes is sufficiently large. However, the convergence rate slows down significantly when the dynamic range of the source amplitudes is large. To bridge this issue, we introduce an adaptive preconditioner design, which compensates for the learning rates of different sources in an iteration-varying manner based on the current estimate. The adaptive design provably leads to an accelerated convergence rate that is independent of the dynamic range, highlighting the benefit of adaptive preconditioning in nonconvex spike deconvolution. Numerical experiments are provided to corroborate the theoretical findings.

Joint Localization and Orientation Estimation in Millimeter-Wave MIMO OFDM Systems via Atomic Norm Minimization

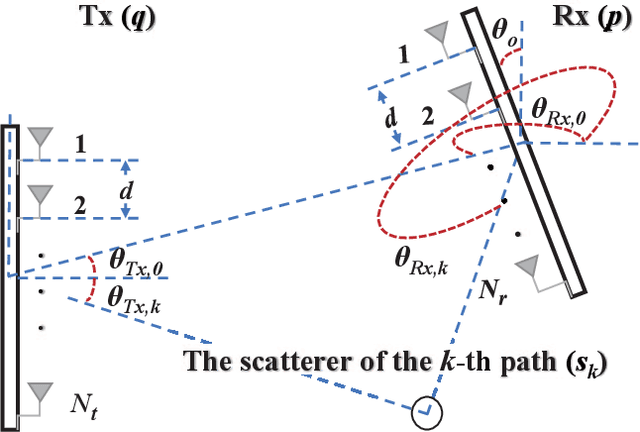
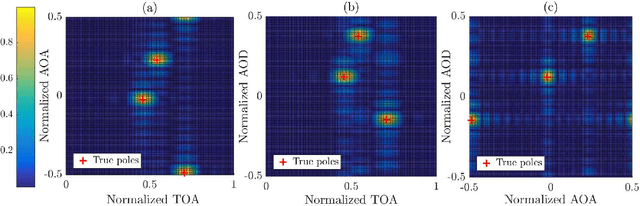
Herein, an atomic norm based method for accurately estimating the location and orientation of a target from millimeter-wave multi-input-multi-output (MIMO) orthogonal frequency-division multiplexing (OFDM) signals is presented. A novel virtual channel matrix is introduced and an algorithm to extract localization-relevant channel parameters from its atomic norm decomposition is designed. Then, based on the extended invariance principle, a weighted least squares problem is proposed to accurately recover the location and orientation using both line-of-sight and non-line-of-sight channel information. The conditions for the optimality and uniqueness of the estimate and theoretical guarantees for the estimation error are characterized for the noiseless and the noisy scenarios. Theoretical results are confirmed via simulation. Numerical results investigate the robustness of the proposed algorithm to incorrect model order selection or synchronization error, and highlight performance improvements over a prior method. The resultant performance nearly achieves the Cramer-Rao lower bound on the estimation error.

On the Stability of Super-Resolution and a Beurling-Selberg Type Extremal Problem

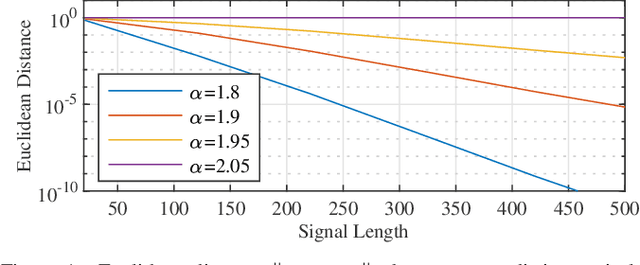
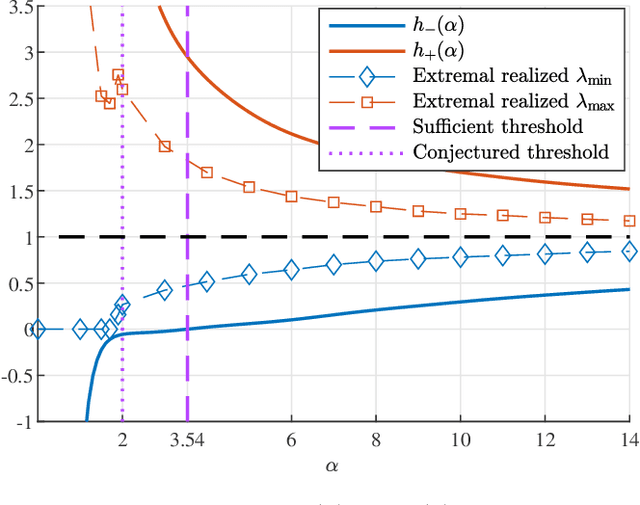
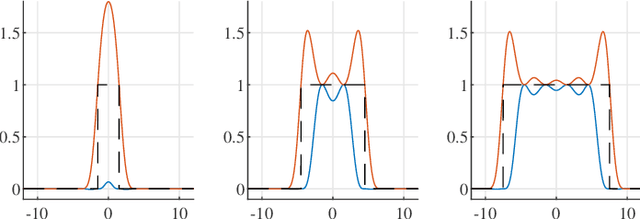
Super-resolution estimation is the problem of recovering a stream of spikes (point sources) from the noisy observation of a few number of its first trigonometric moments. The performance of super-resolution is recognized to be intimately related to the separation between the spikes to recover. A novel notion of stability of the Fisher information matrix (FIM) of the super-resolution problem is introduced, when the minimal eigenvalue of the FIM is not asymptotically vanishing. The regime where the minimal separation is inversely proportional to the number of acquired moments is considered. It is shown that there is a separation threshold above which the eigenvalues of the FIM can be bounded by a quantity that does not depend on the number of moments. The proof relies on characterizing the connection between the stability of the FIM and a generalization of the Beurling-Selberg box approximation problem.

Atomic Norm Based Localization and Orientation Estimation for Millimeter-Wave MIMO OFDM Systems

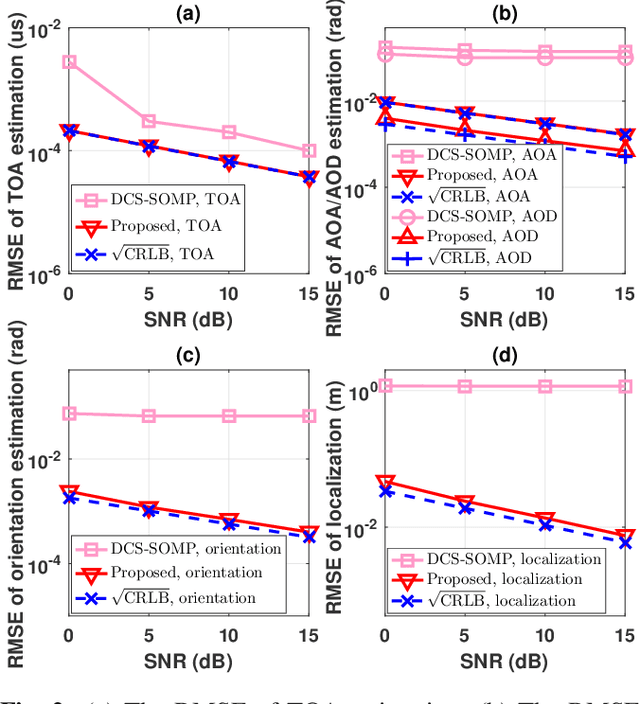
Herein, an atomic norm based method for accurately estimating the location and orientation of a target from millimeter-wave multi-input-multi-output (MIMO) orthogonal frequency-division multiplexing (OFDM) signals is presented. A novel virtual channel matrix is introduced and an algorithm to extract localization-relevant channel parameters from its atomic norm decomposition is designed. Then, based on the extended invariance principle, a weighted least squares problem is proposed to accurately recover the location and orientation using both line-of-sight and non-line-of-sight channel information. Numerical results highlight performance improvements over a prior method and the resultant performance nearly achieves the Cramer-Rao lower bound.

A Framework for Private Communication with Secret Block Structure

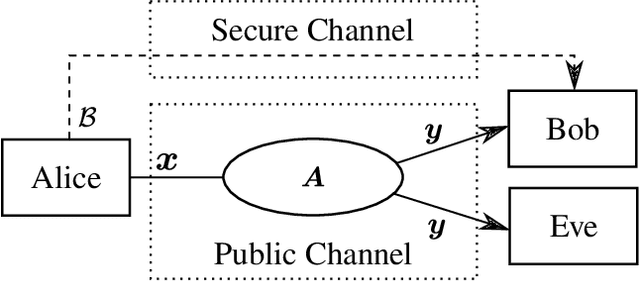
Harnessing a block-sparse prior to recover signals through underdetermined linear measurements has been extensively shown to allow exact recovery in conditions where classical compressed sensing would provably fail. We exploit this result to propose a novel private communication framework where the secrecy is achieved by transmitting instances of an unidentifiable compressed sensing problem over a public channel. The legitimate receiver can attempt to overcome this ill-posedness by leveraging secret knowledge of a block structure that was used to encode the transmitter's message. We study the privacy guarantees of this communication protocol to a single transmission, and to multiple transmissions without refreshing the shared secret. Additionally, we propose an algorithm for an eavesdropper to learn the block structure via the method of moments and highlight the privacy benefits of this framework through numerical experiments.