A Framework for Private Communication with Secret Block Structure
Paper and Code
Oct 08, 2021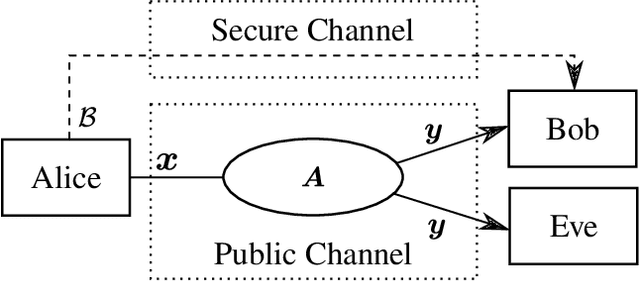
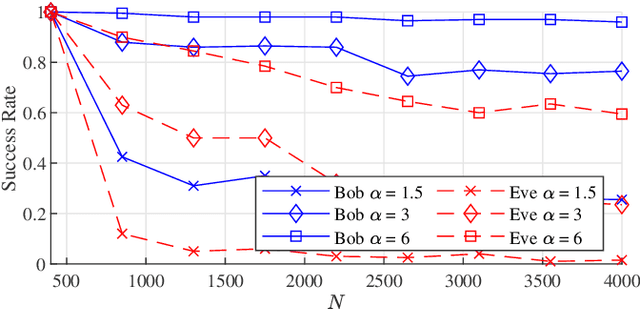

Harnessing a block-sparse prior to recover signals through underdetermined linear measurements has been extensively shown to allow exact recovery in conditions where classical compressed sensing would provably fail. We exploit this result to propose a novel private communication framework where the secrecy is achieved by transmitting instances of an unidentifiable compressed sensing problem over a public channel. The legitimate receiver can attempt to overcome this ill-posedness by leveraging secret knowledge of a block structure that was used to encode the transmitter's message. We study the privacy guarantees of this communication protocol to a single transmission, and to multiple transmissions without refreshing the shared secret. Additionally, we propose an algorithm for an eavesdropper to learn the block structure via the method of moments and highlight the privacy benefits of this framework through numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge