Small-Noise Sensitivity Analysis of Locating Pulses in the Presence of Adversarial Perturbation
Paper and Code
Mar 05, 2024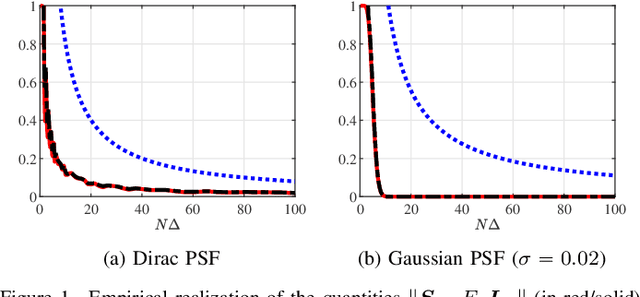
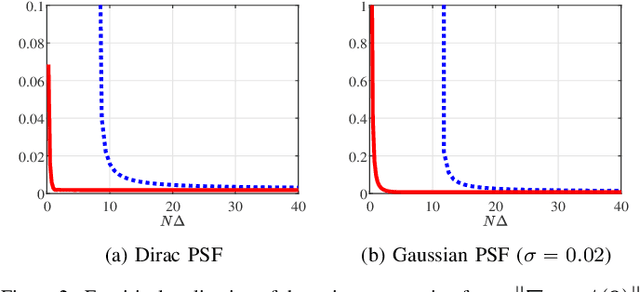
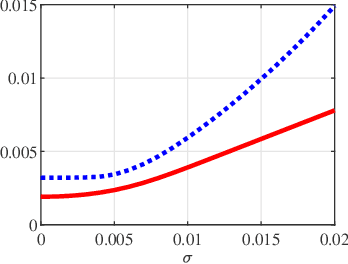
A fundamental small-noise sensitivity analysis of spike localization in the presence of adversarial perturbations and arbitrary point spread function (PSF) is presented. The analysis leverages the local Lipschitz property of the inverse map from measurement noise to parameter estimate. In the small noise regime, the local Lipschitz constant converges to the spectral norm of the noiseless Jacobian of the inverse map. An interpretable upper bound in terms of the minimum separation of spikes, norms, and flatness of the PSF and its derivative, and the distribution of spike amplitudes is provided. Numerical experiments highlighting the relevance of the theoretical bound as a proxy to the local Lipschitz constant and its dependence on the key attributes of the problem are presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge