RED-PSM: Regularization by Denoising of Partially Separable Models for Dynamic Imaging

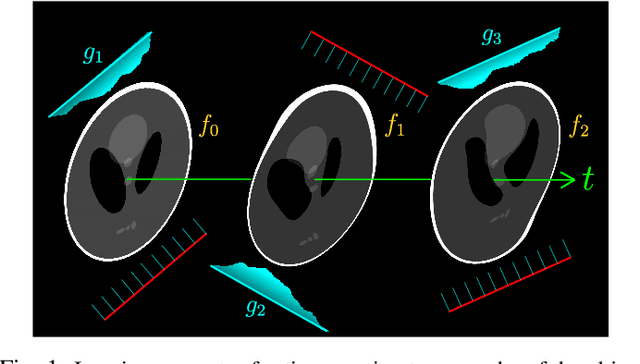
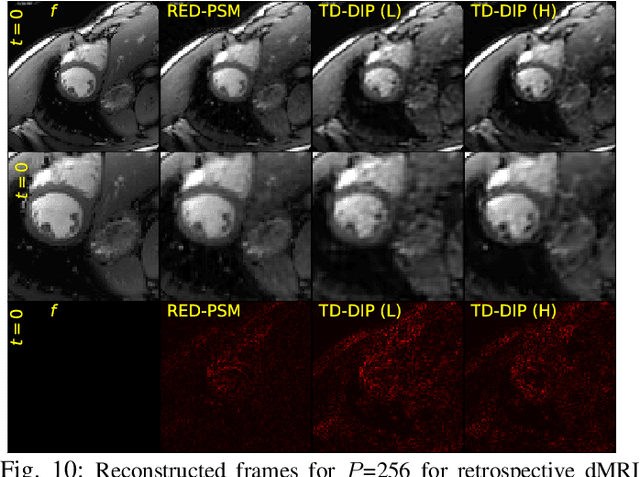
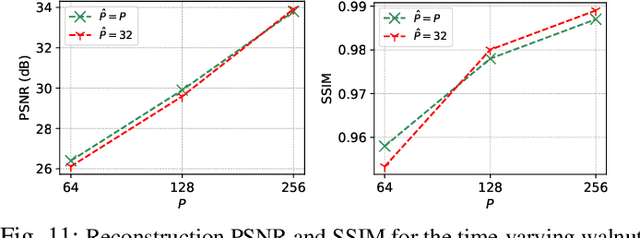
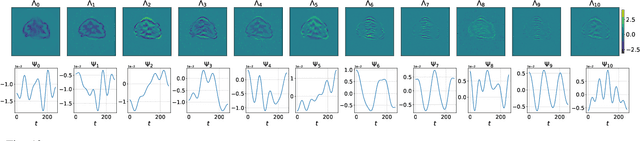
Dynamic imaging addresses the recovery of a time-varying 2D or 3D object at each time instant using its undersampled measurements. In particular, in the case of dynamic tomography, only a single projection at a single view angle may be available at a time, making the problem severely ill-posed. In this work, we propose an approach, RED-PSM, which combines for the first time two powerful techniques to address this challenging imaging problem. The first, are partially separable models, which have been used to efficiently introduce a low-rank prior for the spatio-temporal object. The second is the recent Regularization by Denoising (RED), which provides a flexible framework to exploit the impressive performance of state-of-the-art image denoising algorithms, for various inverse problems. We propose a partially separable objective with RED and an optimization scheme with variable splitting and ADMM, and prove convergence of our objective to a value corresponding to a stationary point satisfying the first order optimality conditions. Convergence is accelerated by a particular projection-domain-based initialization. We demonstrate the performance and computational improvements of our proposed RED-PSM with a learned image denoiser by comparing it to a recent deep-prior-based method TD-DIP.

Dynamic Tomography Reconstruction by Projection-Domain Separable Modeling

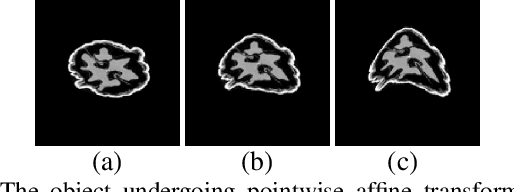
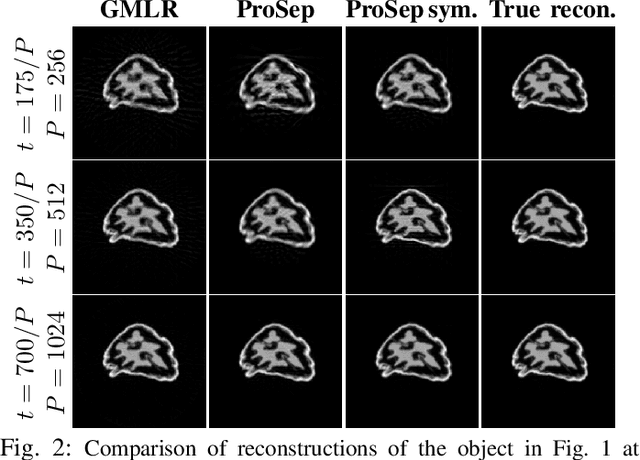
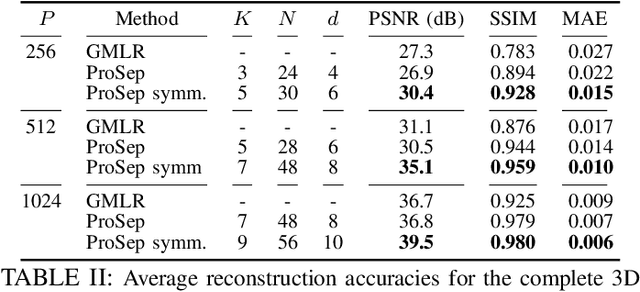
In dynamic tomography the object undergoes changes while projections are being acquired sequentially in time. The resulting inconsistent set of projections cannot be used directly to reconstruct an object corresponding to a time instant. Instead, the objective is to reconstruct a spatio-temporal representation of the object, which can be displayed as a movie. We analyze conditions for unique and stable solution of this ill-posed inverse problem, and present a recovery algorithm, validating it experimentally. We compare our approach to one based on the recently proposed GMLR variation on deep prior for video, demonstrating the advantages of the proposed approach.

Learning to Bound: A Generative Cramér-Rao Bound

The Cram\'er-Rao bound (CRB), a well-known lower bound on the performance of any unbiased parameter estimator, has been used to study a wide variety of problems. However, to obtain the CRB, requires an analytical expression for the likelihood of the measurements given the parameters, or equivalently a precise and explicit statistical model for the data. In many applications, such a model is not available. Instead, this work introduces a novel approach to approximate the CRB using data-driven methods, which removes the requirement for an analytical statistical model. This approach is based on the recent success of deep generative models in modeling complex, high-dimensional distributions. Using a learned normalizing flow model, we model the distribution of the measurements and obtain an approximation of the CRB, which we call Generative Cram\'er-Rao Bound (GCRB). Numerical experiments on simple problems validate this approach, and experiments on two image processing tasks of image denoising and edge detection with a learned camera noise model demonstrate its power and benefits.

Scatter Correction in X-ray CT by Physics-Inspired Deep Learning

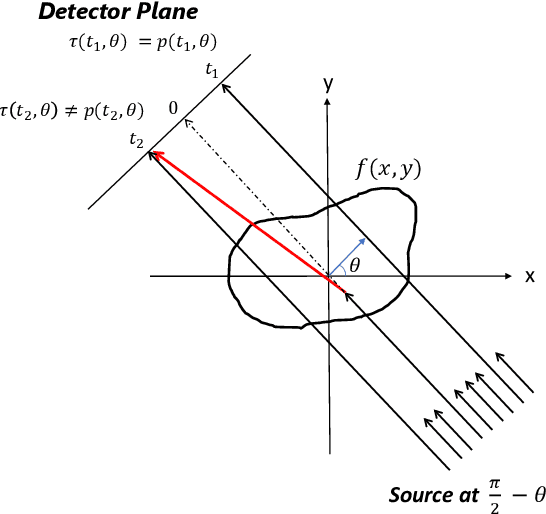
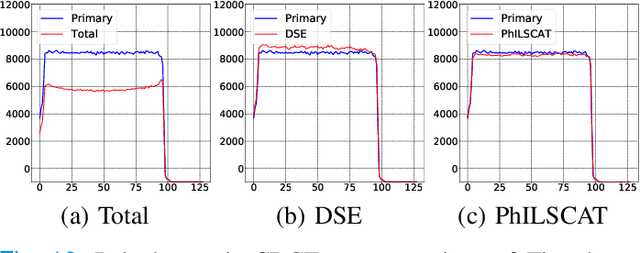
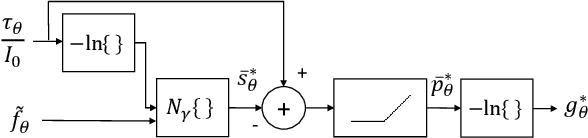
A fundamental problem in X-ray Computed Tomography (CT) is the scatter due to interaction of photons with the imaged object. Unless corrected, scatter manifests itself as degradations in the reconstructions in the form of various artifacts. Scatter correction is therefore critical for reconstruction quality. Scatter correction methods can be divided into two categories: hardware-based; and software-based. Despite success in specific settings, hardware-based methods require modification in the hardware, or increase in the scan time or dose. This makes software-based methods attractive. In this context, Monte-Carlo based scatter estimation, analytical-numerical, and kernel-based methods were developed. Furthermore, data-driven approaches to tackle this problem were recently demonstrated. In this work, two novel physics-inspired deep-learning-based methods, PhILSCAT and OV-PhILSCAT, are proposed. The methods estimate and correct for the scatter in the acquired projection measurements. They incorporate both an initial reconstruction of the object of interest and the scatter-corrupted measurements related to it. They use a common deep neural network architecture and cost function, both tailored to the problem. Numerical experiments with data obtained by Monte-Carlo simulations of the imaging of phantoms reveal significant improvement over a recent purely projection-domain deep neural network scatter correction method.

Circumventing the resolution-time tradeoff in Ultrasound Localization Microscopy by Velocity Filtering

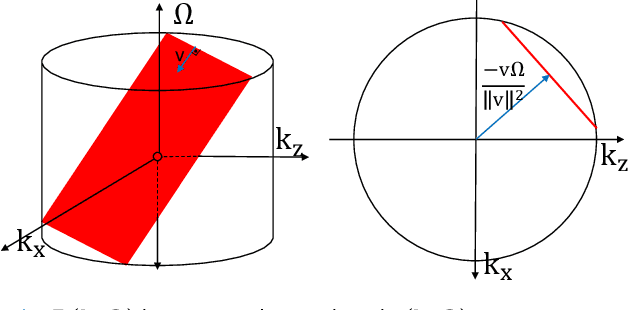
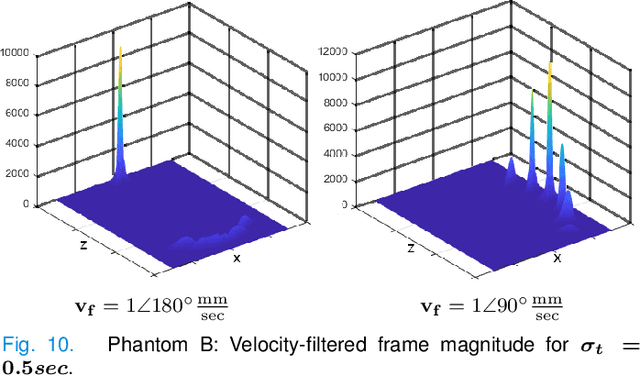
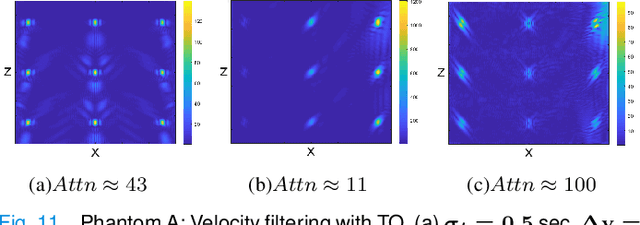
Ultrasound Localization Microscopy (ULM) offers a cost-effective modality for microvascular imaging by using intravascular contrast agents (microbubbles). However, ULM has a fundamental trade-off between acquisition time and spatial resolution, which makes clinical translation challenging. In this paper, in order to circumvent the trade-off, we introduce a spatiotemporal filtering operation dubbed velocity filtering, which is capable of separating contrast agents into different groups based on their vector velocities thus reducing interference in the localization step, while simultaneously offering blood velocity mapping at super resolution, without tracking individual microbubbles. As side benefit, the velocity filter provides noise suppression before microbubble localization that could enable substantially increased penetration depth in tissue typically by 4cm or more. We provide a theoretical analysis of the performance of velocity filter. Numerical experiments confirm that the proposed velocity filter is able to separate the microbubbles with respect to the speed and direction of their motion. In combination with subsequent localization of microbubble centers, e.g. by matched filtering, the velocity filter improves the quality of the reconstructed vasculature significantly and provides blood flow information. Overall, the proposed imaging pipeline in this paper enables the use of higher concentrations of microbubbles while preserving spatial resolution, thus helping circumvent the trade-off between acquisition time and spatial resolution. Conveniently, because the velocity filtering operation can be implemented by fast Fourier transforms(FFTs) it admits fast, and potentially real-time realization. We believe that the proposed velocity filtering method has the potential to pave the way to clinical translation of ULM.

Joint Dimensionality Reduction for Separable Embedding Estimation

Low-dimensional embeddings for data from disparate sources play critical roles in multi-modal machine learning, multimedia information retrieval, and bioinformatics. In this paper, we propose a supervised dimensionality reduction method that learns linear embeddings jointly for two feature vectors representing data of different modalities or data from distinct types of entities. We also propose an efficient feature selection method that complements, and can be applied prior to, our joint dimensionality reduction method. Assuming that there exist true linear embeddings for these features, our analysis of the error in the learned linear embeddings provides theoretical guarantees that the dimensionality reduction method accurately estimates the true embeddings when certain technical conditions are satisfied and the number of samples is sufficiently large. The derived sample complexity results are echoed by numerical experiments. We apply the proposed dimensionality reduction method to gene-disease association, and predict unknown associations using kernel regression on the dimension-reduced feature vectors. Our approach compares favorably against other dimensionality reduction methods, and against a state-of-the-art method of bilinear regression for predicting gene-disease associations.

A Set-Theoretic Study of the Relationships of Image Models and Priors for Restoration Problems

Image prior modeling is the key issue in image recovery, computational imaging, compresses sensing, and other inverse problems. Recent algorithms combining multiple effective priors such as the sparse or low-rank models, have demonstrated superior performance in various applications. However, the relationships among the popular image models are unclear, and no theory in general is available to demonstrate their connections. In this paper, we present a theoretical analysis on the image models, to bridge the gap between applications and image prior understanding, including sparsity, group-wise sparsity, joint sparsity, and low-rankness, etc. We systematically study how effective each image model is for image restoration. Furthermore, we relate the denoising performance improvement by combining multiple models, to the image model relationships. Extensive experiments are conducted to compare the denoising results which are consistent with our analysis. On top of the model-based methods, we quantitatively demonstrate the image properties that are inexplicitly exploited by deep learning method, of which can further boost the denoising performance by combining with its complementary image models.

Improving Robustness of Deep-Learning-Based Image Reconstruction

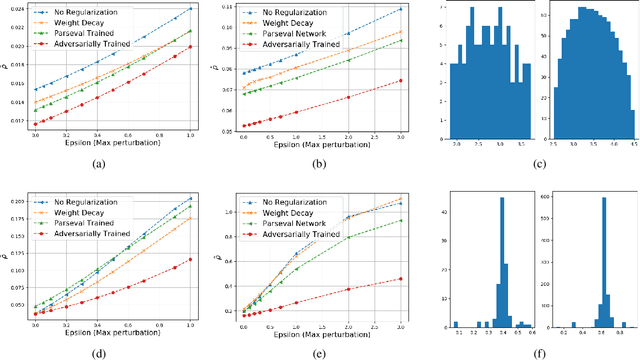
Deep-learning-based methods for different applications have been shown vulnerable to adversarial examples. These examples make deployment of such models in safety-critical tasks questionable. Use of deep neural networks as inverse problem solvers has generated much excitement for medical imaging including CT and MRI, but recently a similar vulnerability has also been demonstrated for these tasks. We show that for such inverse problem solvers, one should analyze and study the effect of adversaries in the measurement-space, instead of the signal-space as in previous work. In this paper, we propose to modify the training strategy of end-to-end deep-learning-based inverse problem solvers to improve robustness. We introduce an auxiliary network to generate adversarial examples, which is used in a min-max formulation to build robust image reconstruction networks. Theoretically, we show for a linear reconstruction scheme the min-max formulation results in a singular-value(s) filter regularized solution, which suppresses the effect of adversarial examples occurring because of ill-conditioning in the measurement matrix. We find that a linear network using the proposed min-max learning scheme indeed converges to the same solution. In addition, for non-linear Compressed Sensing (CS) reconstruction using deep networks, we show significant improvement in robustness using the proposed approach over other methods. We complement the theory by experiments for CS on two different datasets and evaluate the effect of increasing perturbations on trained networks. We find the behavior for ill-conditioned and well-conditioned measurement matrices to be qualitatively different.

Transform Learning for Magnetic Resonance Image Reconstruction: From Model-based Learning to Building Neural Networks

Magnetic resonance imaging (MRI) is widely used in clinical practice for visualizing both biological structure and function, but its use has been traditionally limited by its slow data acquisition. Recent advances in compressed sensing (CS) techniques for MRI that exploit sparsity models of images reduce acquisition time while maintaining high image quality. Whereas classical CS assumes the images are sparse in a known analytical dictionary or transform domain, methods that use learned image models for reconstruction have become popular in recent years. The model could be learned from a dataset and used for reconstruction or learned simultaneously with the reconstruction, a technique called blind CS (BCS). While the well-known synthesis dictionary model has been exploited for MRI reconstruction, recent advances in transform learning (TL) provide an efficient alternative framework for sparse modeling in MRI. TL-based methods enjoy numerous advantages including exact sparse coding, transform update, and clustering solutions, cheap computation, and convergence guarantees, and provide high quality results in MRI as well as in other inverse problems compared to popular competing methods. This paper provides a review of key works in MRI reconstruction from limited data, with focus on the recent class of TL-based reconstruction methods. A unified framework for incorporating various TL-based models is presented. We discuss the connections between transform learning and convolutional or filterbank models and corresponding multi-layer extensions, as well as connections to unsupervised and supervised deep learning. Finally, we discuss recent trends in MRI, open problems, and future directions for the field.

GAN-based Projector for Faster Recovery in Compressed Sensing with Convergence Guarantees

A Generative Adversarial Network (GAN) with generator $G$ trained to model the prior of images has been shown to perform better than sparsity-based regularizers in ill-posed inverse problems. In this work, we propose a new method of deploying a GAN-based prior to solve linear inverse problems using projected gradient descent (PGD). Our method learns a network-based projector for use in the PGD algorithm, eliminating the need for expensive computation of the Jacobian of $G$. Experiments show that our approach provides a speed-up of $30\text{-}40\times$ over earlier GAN-based recovery methods for similar accuracy in compressed sensing. Our main theoretical result is that if the measurement matrix is moderately conditioned for range($G$) and the projector is $\delta$-approximate, then the algorithm is guaranteed to reach $O(\delta)$ reconstruction error in $O(log(1/\delta))$ steps in the low noise regime. Additionally, we propose a fast method to design such measurement matrices for a given $G$. Extensive experiments demonstrate the efficacy of this method by requiring $5\text{-}10\times$ fewer measurements than random Gaussian measurement matrices for comparable recovery performance.