When the Forger Is the Judge: GPT-Image-2 Cannot Recognize Its Own Faked Documents

OpenAI's GPT-Image-2 has effectively erased the visual boundary between authentic and AI-edited document images: a single number on a receipt can be replaced in under a second for a few cents. We release AIForge-Doc v2, a paired dataset of 3,066 GPT-Image-2 document forgeries with pixel-precise masks in DocTamper-compatible format, and benchmark four lines of defence: human inspectors (N=120, n=365 pair-votes via the public 2AFC site CanUSpotAI.com), TruFor (generic forensic), DocTamper (qcf-568, document-specific), and the same GPT-Image-2 model as a zero-shot self-judge -- asked, to avoid the trivial "image is mostly real" reading, whether any region was generated or edited by an AI image model. Human 2AFC accuracy is 0.501, indistinguishable from chance: even side-by-side, inspectors cannot tell GPT-Image-2 receipt forgeries from authentic counterparts. The three computational judges sit only modestly above (TruFor 0.599, DocTamper 0.585, self-judge 0.532). The self-judge fails consistently, not by chance: across five prompt strategies and four policies for handling ambiguous responses, AUC never rises above 0.59. To rule out the possibility that the two forensic detectors are broken on our source domain rather than blind to AI inpainting, we calibrate each on a same-domain traditional-tampering set built for its training distribution: TruFor reaches AUC 0.962 on cross-camera splicing of our dataset, DocTamper reaches 0.852 on cross-document OCR-token splicing with two-pass JPEG re-encoding. Both retain near-published performance on traditional tampering; switching to GPT-Image-2 inpainting drops AUC by 0.27-0.36 (0.962->0.599 TruFor; 0.852->0.585 DocTamper), isolating a detection gap specific to GPT-Image-2 inpainting. We release the dataset, pipeline, four-judge protocol, and calibration sets.

A Synthetic Eye Movement Dataset for Script Reading Detection: Real Trajectory Replay on a 3D Simulator

Large vision-language models have achieved remarkable capabilities by training on massive internet-scale data, yet a fundamental asymmetry persists: while LLMs can leverage self-supervised pretraining on abundant text and image data, the same is not true for many behavioral modalities. Video-based behavioral data -- gestures, eye movements, social signals -- remains scarce, expensive to annotate, and privacy-sensitive. A promising alternative is simulation: replace real data collection with controlled synthetic generation to produce automatically labeled data at scale. We introduce infrastructure for this paradigm applied to eye movement, a behavioral signal with applications across vision-language modeling, virtual reality, robotics, accessibility systems, and cognitive science. We present a pipeline for generating synthetic labeled eye movement video by extracting real human iris trajectories from reference videos and replaying them on a 3D eye movement simulator via headless browser automation. Applying this to the task of script-reading detection during video interviews, we release final_dataset_v1: 144 sessions (72 reading, 72 conversation) totaling 12 hours of synthetic eye movement video at 25fps. Evaluation shows that generated trajectories preserve the temporal dynamics of the source data (KS D < 0.14 across all metrics). A matched frame-by-frame comparison reveals that the 3D simulator exhibits bounded sensitivity at reading-scale movements, attributable to the absence of coupled head movement -- a finding that informs future simulator design. The pipeline, dataset, and evaluation tools are released to support downstream behavioral classifier development at the intersection of behavioral modeling and vision-language systems.

Chinese Language Is Not More Efficient Than English in Vibe Coding: A Preliminary Study on Token Cost and Problem-Solving Rate

A claim has been circulating on social media and practitioner forums that Chinese prompts are more token-efficient than English for LLM coding tasks, potentially reducing costs by up to 40\%. This claim has influenced developers to consider switching to Chinese for ``vibe coding'' to save on API costs. In this paper, we conduct a rigorous empirical study using SWE-bench Lite, a benchmark of software engineering tasks, to evaluate whether this claim of Chinese token efficiency holds up to scrutiny. Our results reveal three key findings: First, the efficiency advantage of Chinese is not observed. Second, token cost varies by model architecture in ways that defy simple assumptions: while MiniMax-2.7 shows 1.28x higher token costs for Chinese, GLM-5 actually consumes fewer tokens with Chinese prompts. Third, and most importantly, we found that the success rate when prompting in Chinese is generally lower than in English across all models we tested. We also measure cost efficiency as expected cost per successful task -- jointly accounting for token consumption and task resolution rate. These findings should be interpreted as preliminary evidence rather than a definitive conclusion, given the limited number of models evaluated and the narrow set of benchmarks tested due to resource constraints; they indicate that language effects on token cost are model-dependent, and that practitioners should not expect cost savings or performance gains just by switching their prompt language to Chinese.

GPT4o-Receipt: A Dataset and Human Study for AI-Generated Document Forensics

Can humans detect AI-generated financial documents better than machines? We present GPT4o-Receipt, a benchmark of 1,235 receipt images pairing GPT-4o-generated receipts with authentic ones from established datasets, evaluated by five state-of-the-art multimodal LLMs and a 30-annotator crowdsourced perceptual study. Our findings reveal a striking paradox: humans are better at seeing AI artifacts, yet worse at detecting AI documents. Human annotators exhibit the largest visual discrimination gap of any evaluator, yet their binary detection F1 falls well below Claude Sonnet 4 and below Gemini 2.5 Flash. This paradox resolves once the mechanism is understood: the dominant forensic signals in AI-generated receipts are arithmetic errors -- invisible to visual inspection but systematically verifiable by LLMs. Humans cannot perceive that a subtotal is incorrect; LLMs verify it in milliseconds. Beyond the human--LLM comparison, our five-model evaluation reveals dramatic performance disparities and calibration differences that render simple accuracy metrics insufficient for detector selection. GPT4o-Receipt, the evaluation framework, and all results are released publicly to support future research in AI document forensics.

Improving Robustness of Deep-Learning-Based Image Reconstruction

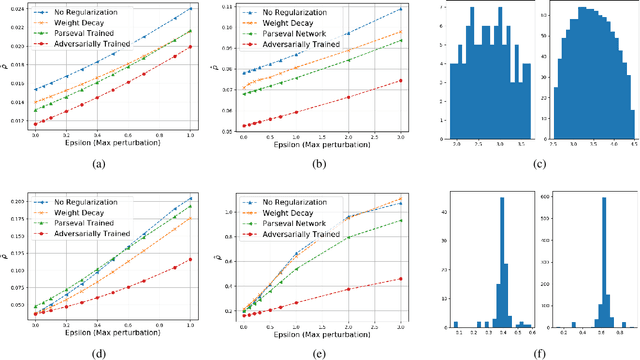
Deep-learning-based methods for different applications have been shown vulnerable to adversarial examples. These examples make deployment of such models in safety-critical tasks questionable. Use of deep neural networks as inverse problem solvers has generated much excitement for medical imaging including CT and MRI, but recently a similar vulnerability has also been demonstrated for these tasks. We show that for such inverse problem solvers, one should analyze and study the effect of adversaries in the measurement-space, instead of the signal-space as in previous work. In this paper, we propose to modify the training strategy of end-to-end deep-learning-based inverse problem solvers to improve robustness. We introduce an auxiliary network to generate adversarial examples, which is used in a min-max formulation to build robust image reconstruction networks. Theoretically, we show for a linear reconstruction scheme the min-max formulation results in a singular-value(s) filter regularized solution, which suppresses the effect of adversarial examples occurring because of ill-conditioning in the measurement matrix. We find that a linear network using the proposed min-max learning scheme indeed converges to the same solution. In addition, for non-linear Compressed Sensing (CS) reconstruction using deep networks, we show significant improvement in robustness using the proposed approach over other methods. We complement the theory by experiments for CS on two different datasets and evaluate the effect of increasing perturbations on trained networks. We find the behavior for ill-conditioned and well-conditioned measurement matrices to be qualitatively different.

GAN-based Projector for Faster Recovery in Compressed Sensing with Convergence Guarantees

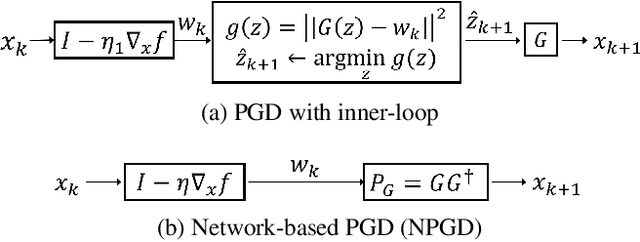
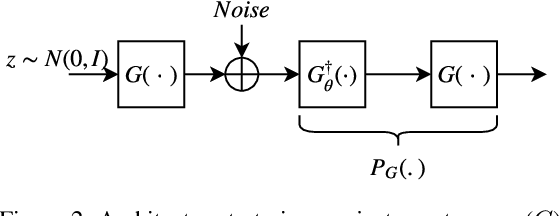
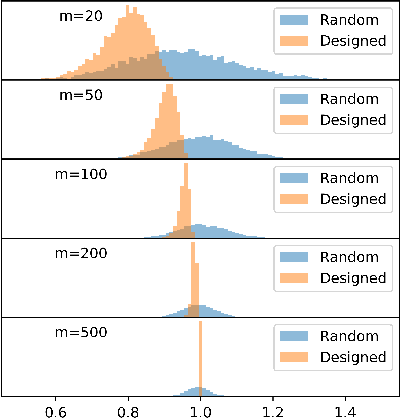
A Generative Adversarial Network (GAN) with generator $G$ trained to model the prior of images has been shown to perform better than sparsity-based regularizers in ill-posed inverse problems. In this work, we propose a new method of deploying a GAN-based prior to solve linear inverse problems using projected gradient descent (PGD). Our method learns a network-based projector for use in the PGD algorithm, eliminating the need for expensive computation of the Jacobian of $G$. Experiments show that our approach provides a speed-up of $30\text{-}40\times$ over earlier GAN-based recovery methods for similar accuracy in compressed sensing. Our main theoretical result is that if the measurement matrix is moderately conditioned for range($G$) and the projector is $\delta$-approximate, then the algorithm is guaranteed to reach $O(\delta)$ reconstruction error in $O(log(1/\delta))$ steps in the low noise regime. Additionally, we propose a fast method to design such measurement matrices for a given $G$. Extensive experiments demonstrate the efficacy of this method by requiring $5\text{-}10\times$ fewer measurements than random Gaussian measurement matrices for comparable recovery performance.