Estimation from Non-Linear Observations via Convex Programming with Application to Bilinear Regression

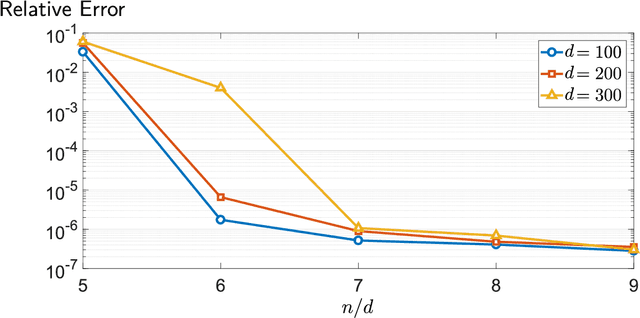
We propose a computationally efficient estimator, formulated as a convex program, for a broad class of non-linear regression problems that involve difference of convex (DC) non-linearities. The proposed method can be viewed as a significant extension of the "anchored regression" method formulated and analyzed in [9] for regression with convex non-linearities. Our main assumption, in addition to other mild statistical and computational assumptions, is availability of a certain approximation oracle for the average of the gradients of the observation functions at a ground truth. Under this assumption and using a PAC-Bayesian analysis we show that the proposed estimator produces an accurate estimate with high probability. As a concrete example, we study the proposed framework in the bilinear regression problem with Gaussian factors and quantify a sufficient sample complexity for exact recovery. Furthermore, we describe a computationally tractable scheme that provably produces the required approximation oracle in the considered bilinear regression problem.