Loop Unrolled Shallow Equilibrium Regularizer (LUSER) -- A Memory-Efficient Inverse Problem Solver
Paper and Code
Oct 10, 2022

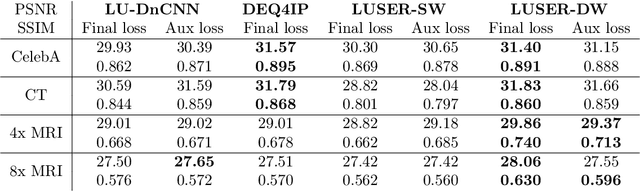

In inverse problems we aim to reconstruct some underlying signal of interest from potentially corrupted and often ill-posed measurements. Classical optimization-based techniques proceed by optimizing a data consistency metric together with a regularizer. Current state-of-the-art machine learning approaches draw inspiration from such techniques by unrolling the iterative updates for an optimization-based solver and then learning a regularizer from data. This loop unrolling (LU) method has shown tremendous success, but often requires a deep model for the best performance leading to high memory costs during training. Thus, to address the balance between computation cost and network expressiveness, we propose an LU algorithm with shallow equilibrium regularizers (LUSER). These implicit models are as expressive as deeper convolutional networks, but far more memory efficient during training. The proposed method is evaluated on image deblurring, computed tomography (CT), as well as single-coil Magnetic Resonance Imaging (MRI) tasks and shows similar, or even better, performance while requiring up to 8 times less computational resources during training when compared against a more typical LU architecture with feedforward convolutional regularizers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge