XAttnMark: Learning Robust Audio Watermarking with Cross-Attention

The rapid proliferation of generative audio synthesis and editing technologies has raised significant concerns about copyright infringement, data provenance, and the spread of misinformation through deepfake audio. Watermarking offers a proactive solution by embedding imperceptible, identifiable, and traceable marks into audio content. While recent neural network-based watermarking methods like WavMark and AudioSeal have improved robustness and quality, they struggle to achieve both robust detection and accurate attribution simultaneously. This paper introduces Cross-Attention Robust Audio Watermark (XAttnMark), which bridges this gap by leveraging partial parameter sharing between the generator and the detector, a cross-attention mechanism for efficient message retrieval, and a temporal conditioning module for improved message distribution. Additionally, we propose a psychoacoustic-aligned temporal-frequency masking loss that captures fine-grained auditory masking effects, enhancing watermark imperceptibility. Our approach achieves state-of-the-art performance in both detection and attribution, demonstrating superior robustness against a wide range of audio transformations, including challenging generative editing with strong editing strength. The project webpage is available at https://liuyixin-louis.github.io/xattnmark/.

PETAL: Physics Emulation Through Averaged Linearizations for Solving Inverse Problems

Inverse problems describe the task of recovering an underlying signal of interest given observables. Typically, the observables are related via some non-linear forward model applied to the underlying unknown signal. Inverting the non-linear forward model can be computationally expensive, as it often involves computing and inverting a linearization at a series of estimates. Rather than inverting the physics-based model, we instead train a surrogate forward model (emulator) and leverage modern auto-grad libraries to solve for the input within a classical optimization framework. Current methods to train emulators are done in a black box supervised machine learning fashion and fail to take advantage of any existing knowledge of the forward model. In this article, we propose a simple learned weighted average model that embeds linearizations of the forward model around various reference points into the model itself, explicitly incorporating known physics. Grounding the learned model with physics based linearizations improves the forward modeling accuracy and provides richer physics based gradient information during the inversion process leading to more accurate signal recovery. We demonstrate the efficacy on an ocean acoustic tomography (OAT) example that aims to recover ocean sound speed profile (SSP) variations from acoustic observations (e.g. eigenray arrival times) within simulation of ocean dynamics in the Gulf of Mexico.

Loop Unrolled Shallow Equilibrium Regularizer (LUSER) -- A Memory-Efficient Inverse Problem Solver

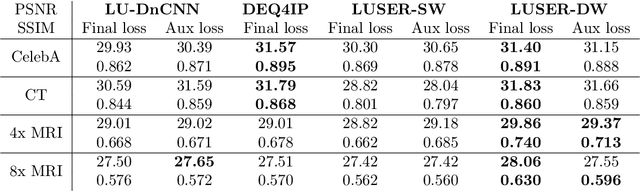
In inverse problems we aim to reconstruct some underlying signal of interest from potentially corrupted and often ill-posed measurements. Classical optimization-based techniques proceed by optimizing a data consistency metric together with a regularizer. Current state-of-the-art machine learning approaches draw inspiration from such techniques by unrolling the iterative updates for an optimization-based solver and then learning a regularizer from data. This loop unrolling (LU) method has shown tremendous success, but often requires a deep model for the best performance leading to high memory costs during training. Thus, to address the balance between computation cost and network expressiveness, we propose an LU algorithm with shallow equilibrium regularizers (LUSER). These implicit models are as expressive as deeper convolutional networks, but far more memory efficient during training. The proposed method is evaluated on image deblurring, computed tomography (CT), as well as single-coil Magnetic Resonance Imaging (MRI) tasks and shows similar, or even better, performance while requiring up to 8 times less computational resources during training when compared against a more typical LU architecture with feedforward convolutional regularizers.