The good, the bad and the ugly sides of data augmentation: An implicit spectral regularization perspective
Paper and Code
Oct 10, 2022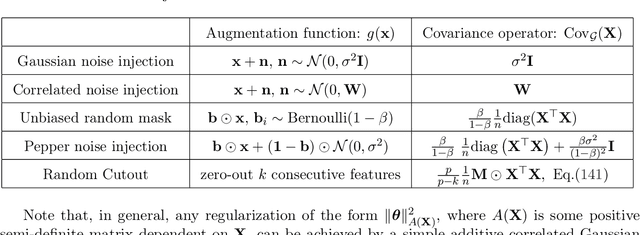
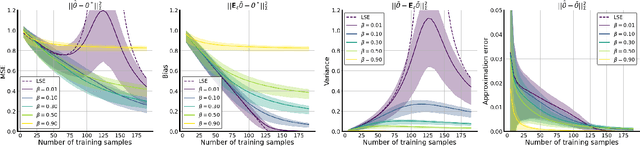
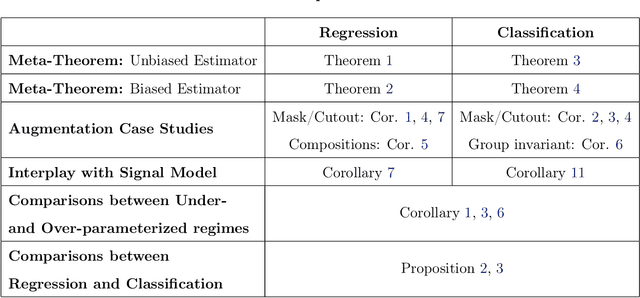
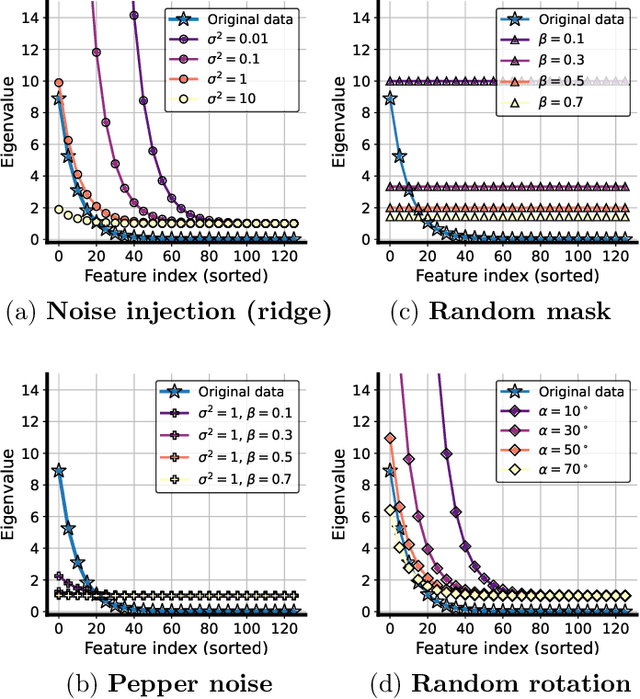
Data augmentation (DA) is a powerful workhorse for bolstering performance in modern machine learning. Specific augmentations like translations and scaling in computer vision are traditionally believed to improve generalization by generating new (artificial) data from the same distribution. However, this traditional viewpoint does not explain the success of prevalent augmentations in modern machine learning (e.g. randomized masking, cutout, mixup), that greatly alter the training data distribution. In this work, we develop a new theoretical framework to characterize the impact of a general class of DA on underparameterized and overparameterized linear model generalization. Our framework reveals that DA induces implicit spectral regularization through a combination of two distinct effects: a) manipulating the relative proportion of eigenvalues of the data covariance matrix in a training-data-dependent manner, and b) uniformly boosting the entire spectrum of the data covariance matrix through ridge regression. These effects, when applied to popular augmentations, give rise to a wide variety of phenomena, including discrepancies in generalization between over-parameterized and under-parameterized regimes and differences between regression and classification tasks. Our framework highlights the nuanced and sometimes surprising impacts of DA on generalization, and serves as a testbed for novel augmentation design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge