Eric Huang
From Behavioral Performance to Internal Competence: Interpreting Vision-Language Models with VLM-Lens
Oct 02, 2025Abstract:We introduce VLM-Lens, a toolkit designed to enable systematic benchmarking, analysis, and interpretation of vision-language models (VLMs) by supporting the extraction of intermediate outputs from any layer during the forward pass of open-source VLMs. VLM-Lens provides a unified, YAML-configurable interface that abstracts away model-specific complexities and supports user-friendly operation across diverse VLMs. It currently supports 16 state-of-the-art base VLMs and their over 30 variants, and is extensible to accommodate new models without changing the core logic. The toolkit integrates easily with various interpretability and analysis methods. We demonstrate its usage with two simple analytical experiments, revealing systematic differences in the hidden representations of VLMs across layers and target concepts. VLM-Lens is released as an open-sourced project to accelerate community efforts in understanding and improving VLMs.
Tuning Algorithmic and Architectural Hyperparameters in Graph-Based Semi-Supervised Learning with Provable Guarantees
Feb 18, 2025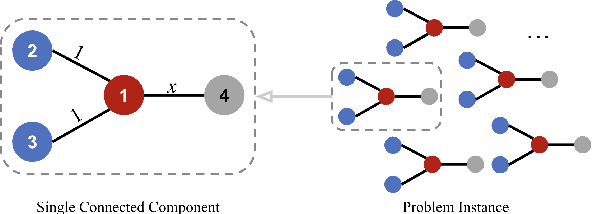

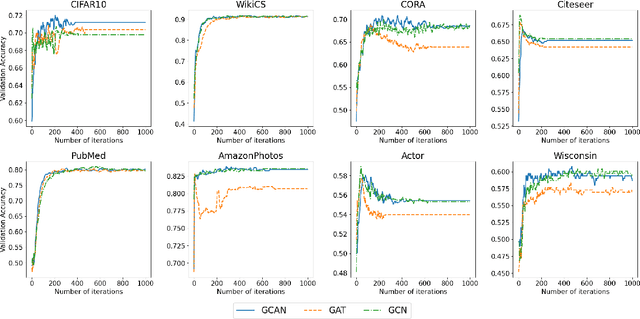
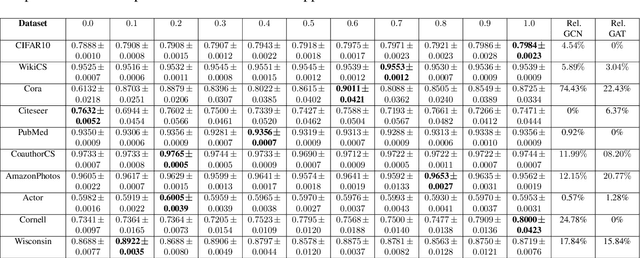
Abstract:Graph-based semi-supervised learning is a powerful paradigm in machine learning for modeling and exploiting the underlying graph structure that captures the relationship between labeled and unlabeled data. A large number of classical as well as modern deep learning based algorithms have been proposed for this problem, often having tunable hyperparameters. We initiate a formal study of tuning algorithm hyperparameters from parameterized algorithm families for this problem. We obtain novel $O(\log n)$ pseudo-dimension upper bounds for hyperparameter selection in three classical label propagation-based algorithm families, where $n$ is the number of nodes, implying bounds on the amount of data needed for learning provably good parameters. We further provide matching $\Omega(\log n)$ pseudo-dimension lower bounds, thus asymptotically characterizing the learning-theoretic complexity of the parameter tuning problem. We extend our study to selecting architectural hyperparameters in modern graph neural networks. We bound the Rademacher complexity for tuning the self-loop weighting in recently proposed Simplified Graph Convolution (SGC) networks. We further propose a tunable architecture that interpolates graph convolutional neural networks (GCN) and graph attention networks (GAT) in every layer, and provide Rademacher complexity bounds for tuning the interpolation coefficient.
Real-time Digital RF Emulation -- I: The Direct Path Computational Model
Jun 13, 2024



Abstract:In this paper we consider the problem of developing a computational model for emulating an RF channel. The motivation for this is that an accurate and scalable emulator has the potential to minimize the need for field testing, which is expensive, slow, and difficult to replicate. Traditionally, emulators are built using a tapped delay line model where long filters modeling the physical interactions of objects are implemented directly. For an emulation scenario consisting of $M$ objects all interacting with one another, the tapped delay line model's computational requirements scale as $O(M^3)$ per sample: there are $O(M^2)$ channels, each with $O(M)$ complexity. In this paper, we develop a new ``direct path" model that, while remaining physically faithful, allows us to carefully factor the emulator operations, resulting in an $O(M^2)$ per sample scaling of the computational requirements. The impact of this is drastic, a $200$ object scenario sees about a $100\times$ reduction in the number of per sample computations. Furthermore, the direct path model gives us a natural way to distribute the computations for an emulation: each object is mapped to a computational node, and these nodes are networked in a fully connected communication graph. Alongside a discussion of the model and the physical phenomena it emulates, we show how to efficiently parameterize antenna responses and scattering profiles within this direct path framework. To verify the model and demonstrate its viability in hardware, we provide several numerical experiments produced using a cycle level C++ simulator of a hardware implementation of the model.
Contact Mode Guided Motion Planning for Dexterous Manipulation
May 30, 2021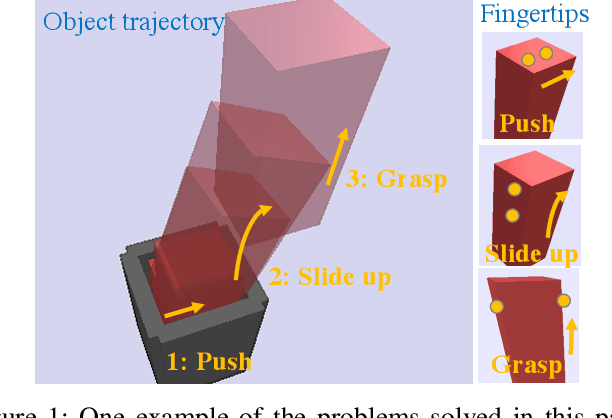

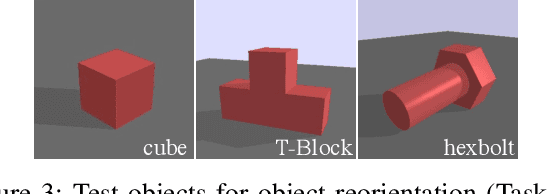

Abstract:Within the field of robotic manipulation, a central goal is to replicate the human ability to manipulate any object in any situation using a sequence of manipulation primitives such as grasping, pushing, inserting, sliding, etc. Conceptually, each manipulation primitive restricts the object and robot to move on a lower-dimensional manifold defined by the primitive's dynamic equations of motion. Likewise, a manipulation sequence represents a dynamically feasible trajectory that traverses multiple manifolds. To manipulate any object in any situation, robotic systems must include the ability to automatically synthesize manipulation primitives (manifolds) and sequence those primitives into a coherent plan (find a path across the manifolds). This paper investigates a principled approach for solving dexterous manipulation planning. This approach is based on rapidly-exploring random trees which use contact modes to guide tree expansion along primitive manifolds. This paper extends this algorithm from 2D domains to 3D domains. We validated our algorithm on a large collection of simulated 3D manipulation tasks. These tasks required our algorithm to sequence between 6-42 manipulation primitives (i.e.\! distinct contact modes). We believe this work represents an important step towards robotic manipulation capabilities which generalize across objects and environments.
Contact Mode Guided Sampling-Based Planning for Quasistatic Dexterous Manipulation in 2D
Nov 03, 2020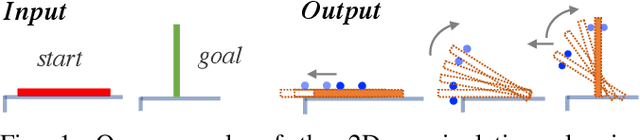
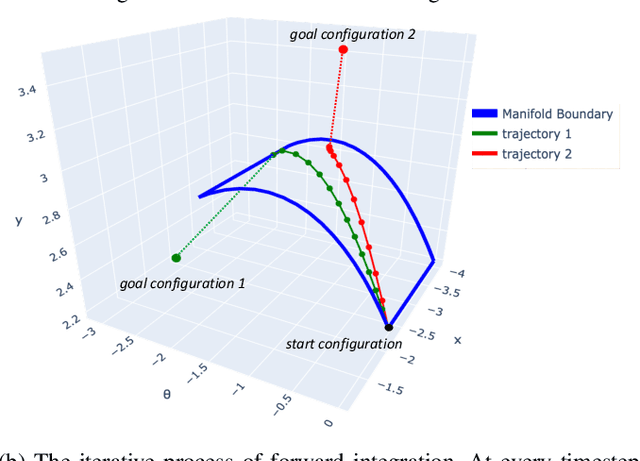


Abstract:The discontinuities and multi-modality introduced by contacts make manipulation planning challenging. Many previous works avoid this problem by pre-designing a set of high-level motion primitives like grasping and pushing. However, such motion primitives are often not adequate to describe dexterous manipulation motions. In this work, we propose a method for automatic dexterous manipulation planning at a more primitive level. The key idea is to use contact modes to guide the search in a sampling-based planning framework. Our method can automatically generate contact transitions and motion trajectories under the quasistatic assumption. In the experiments, this method sometimes generates motions that are often pre-designed as motion primitives, as well as dexterous motions that are more task-specific.
Optimal Rectangle Packing: An Absolute Placement Approach
Feb 04, 2014
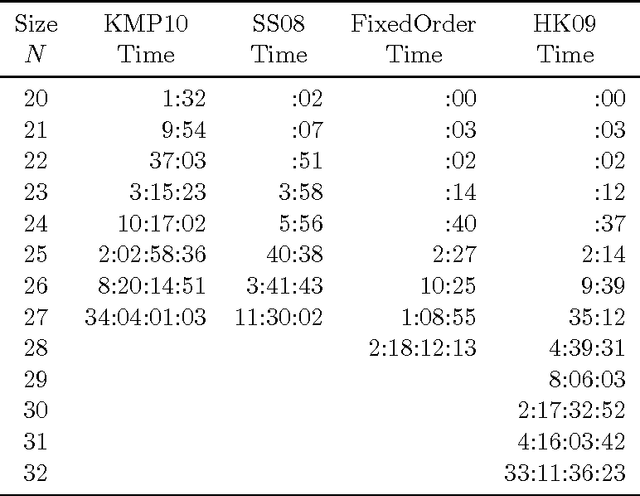
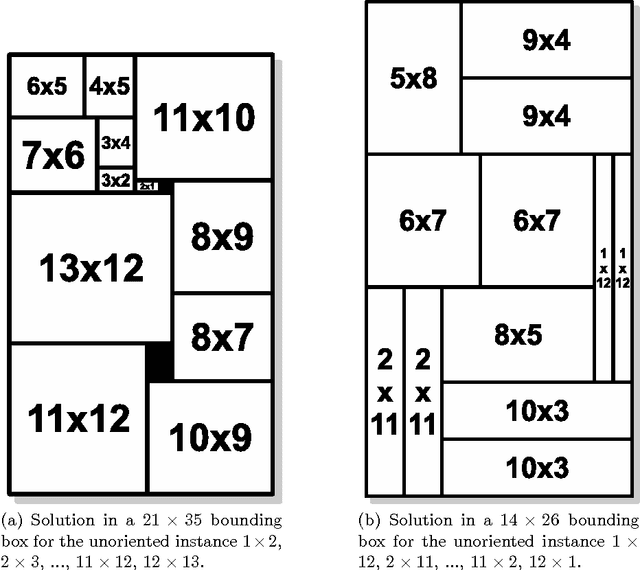
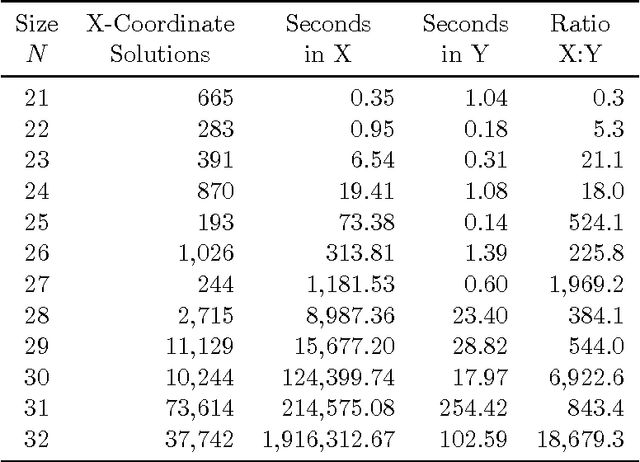
Abstract:We consider the problem of finding all enclosing rectangles of minimum area that can contain a given set of rectangles without overlap. Our rectangle packer chooses the x-coordinates of all the rectangles before any of the y-coordinates. We then transform the problem into a perfect-packing problem with no empty space by adding additional rectangles. To determine the y-coordinates, we branch on the different rectangles that can be placed in each empty position. Our packer allows us to extend the known solutions for a consecutive-square benchmark from 27 to 32 squares. We also introduce three new benchmarks, avoiding properties that make a benchmark easy, such as rectangles with shared dimensions. Our third benchmark consists of rectangles of increasingly high precision. To pack them efficiently, we limit the rectangles coordinates and the bounding box dimensions to the set of subset sums of the rectangles dimensions. Overall, our algorithms represent the current state-of-the-art for this problem, outperforming other algorithms by orders of magnitude, depending on the benchmark.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge