Tuning Algorithmic and Architectural Hyperparameters in Graph-Based Semi-Supervised Learning with Provable Guarantees
Paper and Code
Feb 18, 2025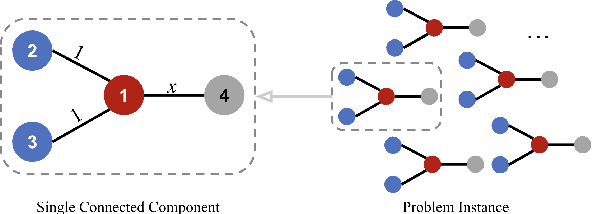

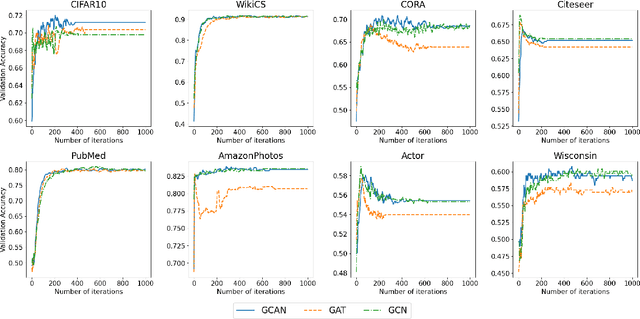
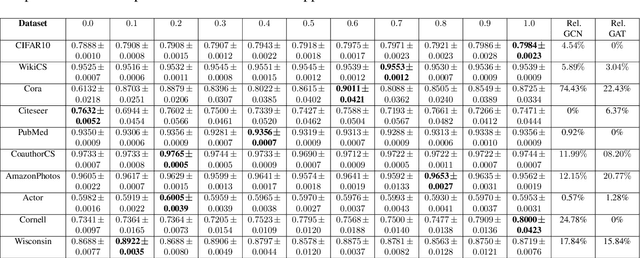
Graph-based semi-supervised learning is a powerful paradigm in machine learning for modeling and exploiting the underlying graph structure that captures the relationship between labeled and unlabeled data. A large number of classical as well as modern deep learning based algorithms have been proposed for this problem, often having tunable hyperparameters. We initiate a formal study of tuning algorithm hyperparameters from parameterized algorithm families for this problem. We obtain novel $O(\log n)$ pseudo-dimension upper bounds for hyperparameter selection in three classical label propagation-based algorithm families, where $n$ is the number of nodes, implying bounds on the amount of data needed for learning provably good parameters. We further provide matching $\Omega(\log n)$ pseudo-dimension lower bounds, thus asymptotically characterizing the learning-theoretic complexity of the parameter tuning problem. We extend our study to selecting architectural hyperparameters in modern graph neural networks. We bound the Rademacher complexity for tuning the self-loop weighting in recently proposed Simplified Graph Convolution (SGC) networks. We further propose a tunable architecture that interpolates graph convolutional neural networks (GCN) and graph attention networks (GAT) in every layer, and provide Rademacher complexity bounds for tuning the interpolation coefficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge