Tuning Algorithmic and Architectural Hyperparameters in Graph-Based Semi-Supervised Learning with Provable Guarantees

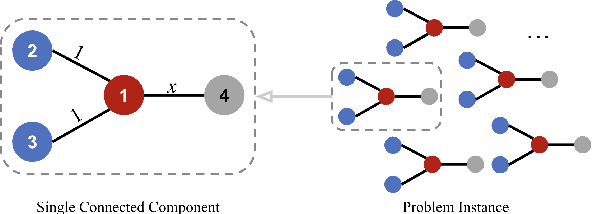
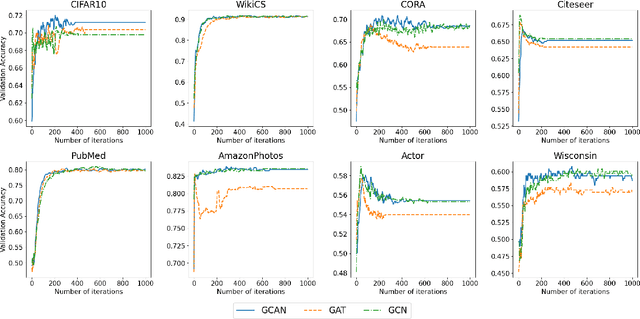
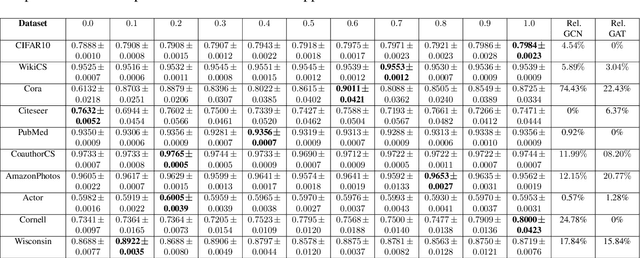
Graph-based semi-supervised learning is a powerful paradigm in machine learning for modeling and exploiting the underlying graph structure that captures the relationship between labeled and unlabeled data. A large number of classical as well as modern deep learning based algorithms have been proposed for this problem, often having tunable hyperparameters. We initiate a formal study of tuning algorithm hyperparameters from parameterized algorithm families for this problem. We obtain novel $O(\log n)$ pseudo-dimension upper bounds for hyperparameter selection in three classical label propagation-based algorithm families, where $n$ is the number of nodes, implying bounds on the amount of data needed for learning provably good parameters. We further provide matching $\Omega(\log n)$ pseudo-dimension lower bounds, thus asymptotically characterizing the learning-theoretic complexity of the parameter tuning problem. We extend our study to selecting architectural hyperparameters in modern graph neural networks. We bound the Rademacher complexity for tuning the self-loop weighting in recently proposed Simplified Graph Convolution (SGC) networks. We further propose a tunable architecture that interpolates graph convolutional neural networks (GCN) and graph attention networks (GAT) in every layer, and provide Rademacher complexity bounds for tuning the interpolation coefficient.

Misspecified $Q$-Learning with Sparse Linear Function Approximation: Tight Bounds on Approximation Error

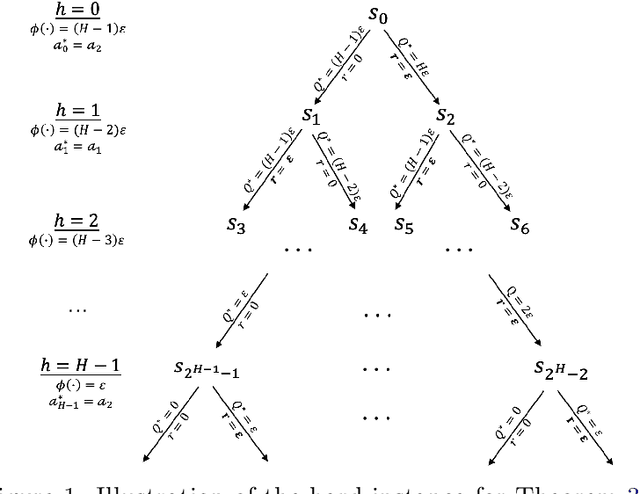
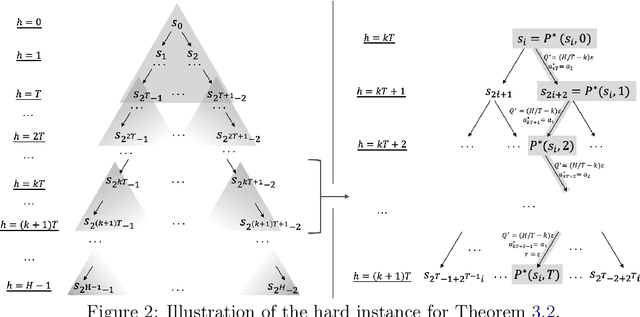
The recent work by Dong & Yang (2023) showed for misspecified sparse linear bandits, one can obtain an $O\left(\epsilon\right)$-optimal policy using a polynomial number of samples when the sparsity is a constant, where $\epsilon$ is the misspecification error. This result is in sharp contrast to misspecified linear bandits without sparsity, which require an exponential number of samples to get the same guarantee. In order to study whether the analog result is possible in the reinforcement learning setting, we consider the following problem: assuming the optimal $Q$-function is a $d$-dimensional linear function with sparsity $k$ and misspecification error $\epsilon$, whether we can obtain an $O\left(\epsilon\right)$-optimal policy using number of samples polynomially in the feature dimension $d$. We first demonstrate why the standard approach based on Bellman backup or the existing optimistic value function elimination approach such as OLIVE (Jiang et al., 2017) achieves suboptimal guarantees for this problem. We then design a novel elimination-based algorithm to show one can obtain an $O\left(H\epsilon\right)$-optimal policy with sample complexity polynomially in the feature dimension $d$ and planning horizon $H$. Lastly, we complement our upper bound with an $\widetilde{\Omega}\left(H\epsilon\right)$ suboptimality lower bound, giving a complete picture of this problem.

Reconciling Model Multiplicity for Downstream Decision Making

We consider the problem of model multiplicity in downstream decision-making, a setting where two predictive models of equivalent accuracy cannot agree on the best-response action for a downstream loss function. We show that even when the two predictive models approximately agree on their individual predictions almost everywhere, it is still possible for their induced best-response actions to differ on a substantial portion of the population. We address this issue by proposing a framework that calibrates the predictive models with regard to both the downstream decision-making problem and the individual probability prediction. Specifically, leveraging tools from multi-calibration, we provide an algorithm that, at each time-step, first reconciles the differences in individual probability prediction, then calibrates the updated models such that they are indistinguishable from the true probability distribution to the decision-maker. We extend our results to the setting where one does not have direct access to the true probability distribution and instead relies on a set of i.i.d data to be the empirical distribution. Finally, we provide a set of experiments to empirically evaluate our methods: compared to existing work, our proposed algorithm creates a pair of predictive models with both improved downstream decision-making losses and agrees on their best-response actions almost everywhere.