Reconciling Model Multiplicity for Downstream Decision Making

We consider the problem of model multiplicity in downstream decision-making, a setting where two predictive models of equivalent accuracy cannot agree on the best-response action for a downstream loss function. We show that even when the two predictive models approximately agree on their individual predictions almost everywhere, it is still possible for their induced best-response actions to differ on a substantial portion of the population. We address this issue by proposing a framework that calibrates the predictive models with regard to both the downstream decision-making problem and the individual probability prediction. Specifically, leveraging tools from multi-calibration, we provide an algorithm that, at each time-step, first reconciles the differences in individual probability prediction, then calibrates the updated models such that they are indistinguishable from the true probability distribution to the decision-maker. We extend our results to the setting where one does not have direct access to the true probability distribution and instead relies on a set of i.i.d data to be the empirical distribution. Finally, we provide a set of experiments to empirically evaluate our methods: compared to existing work, our proposed algorithm creates a pair of predictive models with both improved downstream decision-making losses and agrees on their best-response actions almost everywhere.

Federated Learning as a Network Effects Game

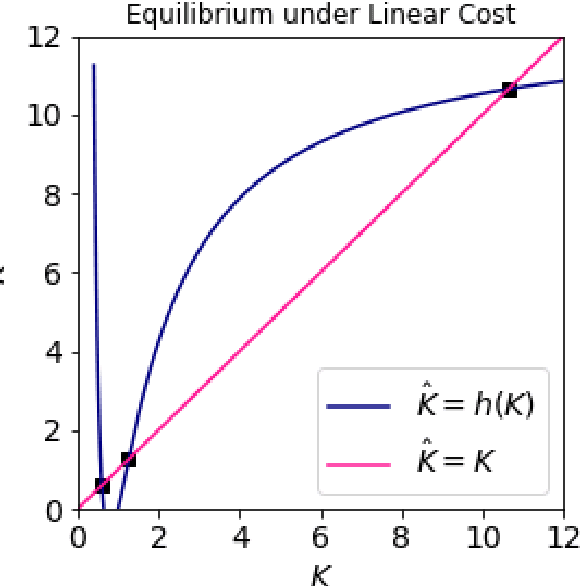
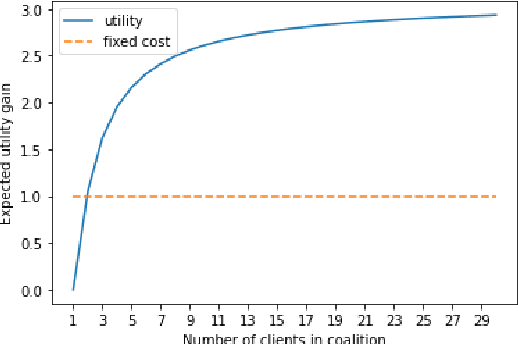
Federated Learning (FL) aims to foster collaboration among a population of clients to improve the accuracy of machine learning without directly sharing local data. Although there has been rich literature on designing federated learning algorithms, most prior works implicitly assume that all clients are willing to participate in a FL scheme. In practice, clients may not benefit from joining in FL, especially in light of potential costs related to issues such as privacy and computation. In this work, we study the clients' incentives in federated learning to help the service provider design better solutions and ensure clients make better decisions. We are the first to model clients' behaviors in FL as a network effects game, where each client's benefit depends on other clients who also join the network. Using this setup we analyze the dynamics of clients' participation and characterize the equilibrium, where no client has incentives to alter their decision. Specifically, we show that dynamics in the population naturally converge to equilibrium without needing explicit interventions. Finally, we provide a cost-efficient payment scheme that incentivizes clients to reach a desired equilibrium when the initial network is empty.

Incentivizing Combinatorial Bandit Exploration

Consider a bandit algorithm that recommends actions to self-interested users in a recommendation system. The users are free to choose other actions and need to be incentivized to follow the algorithm's recommendations. While the users prefer to exploit, the algorithm can incentivize them to explore by leveraging the information collected from the previous users. All published work on this problem, known as incentivized exploration, focuses on small, unstructured action sets and mainly targets the case when the users' beliefs are independent across actions. However, realistic exploration problems often feature large, structured action sets and highly correlated beliefs. We focus on a paradigmatic exploration problem with structure: combinatorial semi-bandits. We prove that Thompson Sampling, when applied to combinatorial semi-bandits, is incentive-compatible when initialized with a sufficient number of samples of each arm (where this number is determined in advance by the Bayesian prior). Moreover, we design incentive-compatible algorithms for collecting the initial samples.

Improved Regret for Differentially Private Exploration in Linear MDP

We study privacy-preserving exploration in sequential decision-making for environments that rely on sensitive data such as medical records. In particular, we focus on solving the problem of reinforcement learning (RL) subject to the constraint of (joint) differential privacy in the linear MDP setting, where both dynamics and rewards are given by linear functions. Prior work on this problem due to Luyo et al. (2021) achieves a regret rate that has a dependence of $O(K^{3/5})$ on the number of episodes $K$. We provide a private algorithm with an improved regret rate with an optimal dependence of $O(\sqrt{K})$ on the number of episodes. The key recipe for our stronger regret guarantee is the adaptivity in the policy update schedule, in which an update only occurs when sufficient changes in the data are detected. As a result, our algorithm benefits from low switching cost and only performs $O(\log(K))$ updates, which greatly reduces the amount of privacy noise. Finally, in the most prevalent privacy regimes where the privacy parameter $\epsilon$ is a constant, our algorithm incurs negligible privacy cost -- in comparison with the existing non-private regret bounds, the additional regret due to privacy appears in lower-order terms.