Shuran Zheng
Truthful Dataset Valuation by Pointwise Mutual Information
May 28, 2024Abstract:A common way to evaluate a dataset in ML involves training a model on this dataset and assessing the model's performance on a test set. However, this approach has two issues: (1) it may incentivize undesirable data manipulation in data marketplaces, as the self-interested data providers seek to modify the dataset to maximize their evaluation scores; (2) it may select datasets that overfit to potentially small test sets. We propose a new data valuation method that provably guarantees the following: data providers always maximize their expected score by truthfully reporting their observed data. Any manipulation of the data, including but not limited to data duplication, adding random data, data removal, or re-weighting data from different groups, cannot increase their expected score. Our method, following the paradigm of proper scoring rules, measures the pointwise mutual information (PMI) of the test dataset and the evaluated dataset. However, computing the PMI of two datasets is challenging. We introduce a novel PMI measuring method that greatly improves tractability within Bayesian machine learning contexts. This is accomplished through a new characterization of PMI that relies solely on the posterior probabilities of the model parameter at an arbitrarily selected value. Finally, we support our theoretical results with simulations and further test the effectiveness of our data valuation method in identifying the top datasets among multiple data providers. Interestingly, our method outperforms the standard approach of selecting datasets based on the trained model's test performance, suggesting that our truthful valuation score can also be more robust to overfitting.
Federated Learning as a Network Effects Game
Feb 16, 2023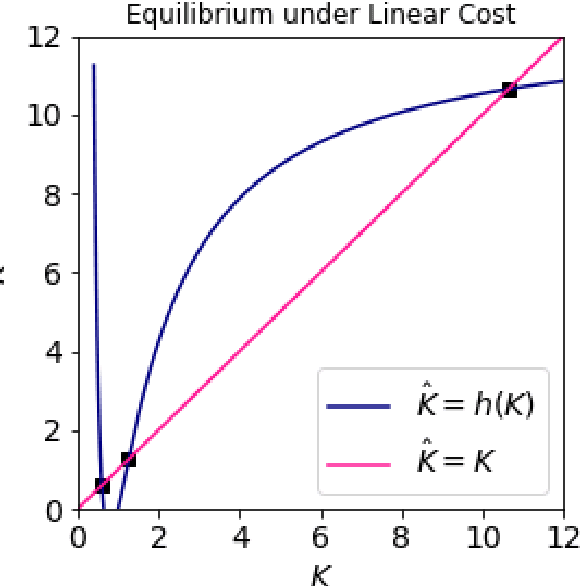
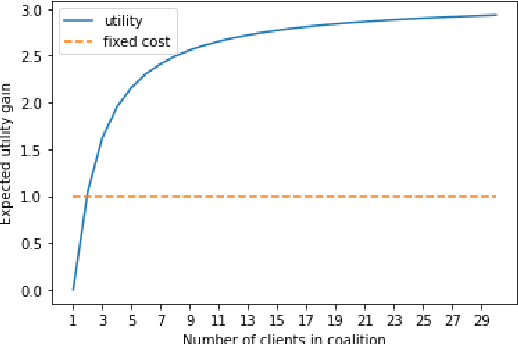
Abstract:Federated Learning (FL) aims to foster collaboration among a population of clients to improve the accuracy of machine learning without directly sharing local data. Although there has been rich literature on designing federated learning algorithms, most prior works implicitly assume that all clients are willing to participate in a FL scheme. In practice, clients may not benefit from joining in FL, especially in light of potential costs related to issues such as privacy and computation. In this work, we study the clients' incentives in federated learning to help the service provider design better solutions and ensure clients make better decisions. We are the first to model clients' behaviors in FL as a network effects game, where each client's benefit depends on other clients who also join the network. Using this setup we analyze the dynamics of clients' participation and characterize the equilibrium, where no client has incentives to alter their decision. Specifically, we show that dynamics in the population naturally converge to equilibrium without needing explicit interventions. Finally, we provide a cost-efficient payment scheme that incentivizes clients to reach a desired equilibrium when the initial network is empty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge