Misspecified $Q$-Learning with Sparse Linear Function Approximation: Tight Bounds on Approximation Error

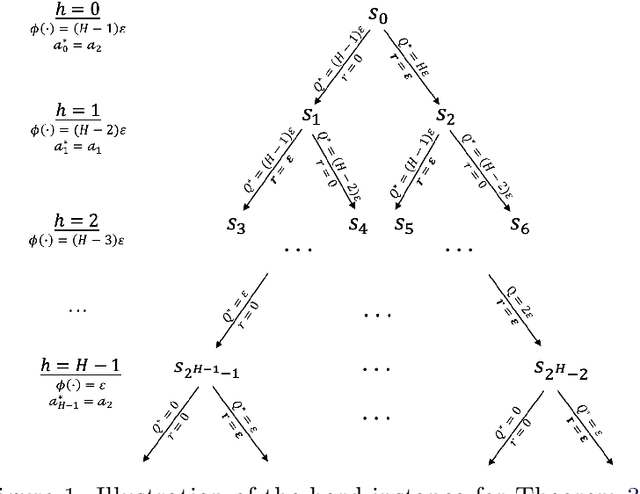
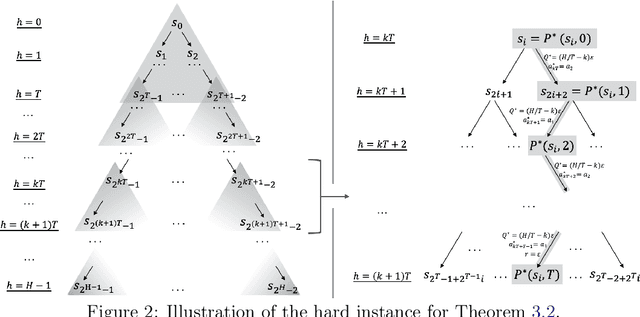
The recent work by Dong & Yang (2023) showed for misspecified sparse linear bandits, one can obtain an $O\left(\epsilon\right)$-optimal policy using a polynomial number of samples when the sparsity is a constant, where $\epsilon$ is the misspecification error. This result is in sharp contrast to misspecified linear bandits without sparsity, which require an exponential number of samples to get the same guarantee. In order to study whether the analog result is possible in the reinforcement learning setting, we consider the following problem: assuming the optimal $Q$-function is a $d$-dimensional linear function with sparsity $k$ and misspecification error $\epsilon$, whether we can obtain an $O\left(\epsilon\right)$-optimal policy using number of samples polynomially in the feature dimension $d$. We first demonstrate why the standard approach based on Bellman backup or the existing optimistic value function elimination approach such as OLIVE (Jiang et al., 2017) achieves suboptimal guarantees for this problem. We then design a novel elimination-based algorithm to show one can obtain an $O\left(H\epsilon\right)$-optimal policy with sample complexity polynomially in the feature dimension $d$ and planning horizon $H$. Lastly, we complement our upper bound with an $\widetilde{\Omega}\left(H\epsilon\right)$ suboptimality lower bound, giving a complete picture of this problem.