A*+BFHS: A Hybrid Heuristic Search Algorithm

We present a new algorithm A*+BFHS for solving hard problems where A* and IDA* fail due to memory limitations and/or the existence of many short cycles. A*+BFHS is based on A* and breadth-first heuristic search (BFHS). A*+BFHS combines advantages from both algorithms, namely A*'s node ordering, BFHS's memory savings, and both algorithms' duplicate detection. On easy problems, A*+BFHS behaves the same as A*. On hard problems, it is slower than A* but saves a large amount of memory. Compared to BFIDA*, A*+BFHS reduces the search time and/or memory requirement by several times on a variety of planning domains.

Optimal Rectangle Packing: An Absolute Placement Approach

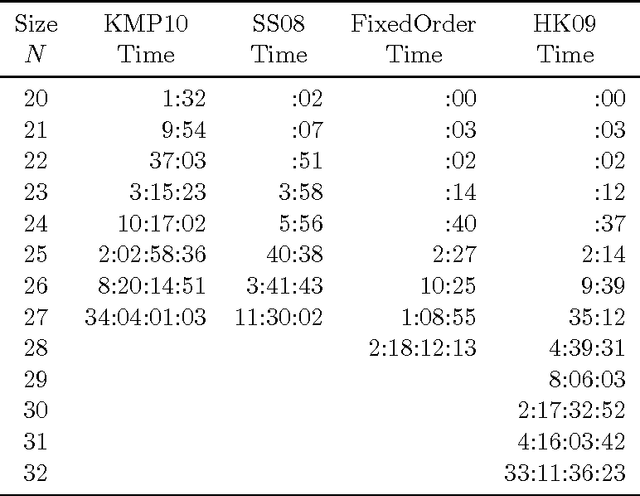
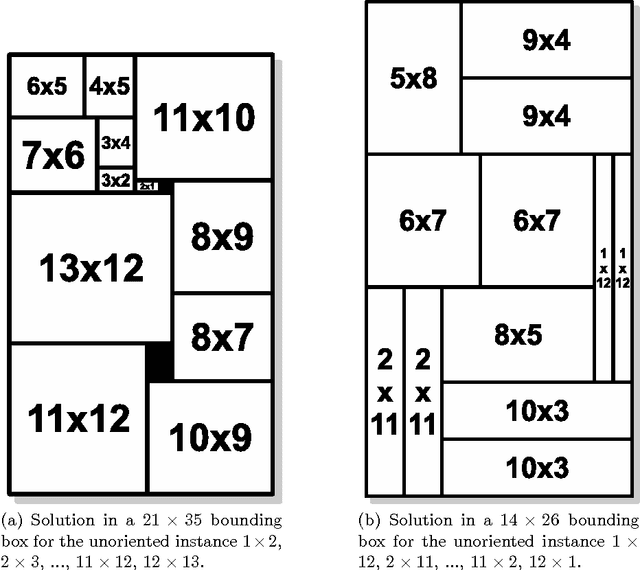
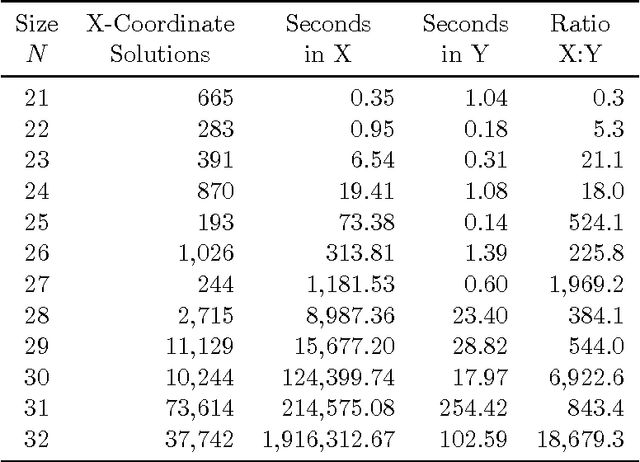
We consider the problem of finding all enclosing rectangles of minimum area that can contain a given set of rectangles without overlap. Our rectangle packer chooses the x-coordinates of all the rectangles before any of the y-coordinates. We then transform the problem into a perfect-packing problem with no empty space by adding additional rectangles. To determine the y-coordinates, we branch on the different rectangles that can be placed in each empty position. Our packer allows us to extend the known solutions for a consecutive-square benchmark from 27 to 32 squares. We also introduce three new benchmarks, avoiding properties that make a benchmark easy, such as rectangles with shared dimensions. Our third benchmark consists of rectangles of increasingly high precision. To pack them efficiently, we limit the rectangles coordinates and the bounding box dimensions to the set of subset sums of the rectangles dimensions. Overall, our algorithms represent the current state-of-the-art for this problem, outperforming other algorithms by orders of magnitude, depending on the benchmark.