Contact Mode Guided Motion Planning for Dexterous Manipulation
Paper and Code
May 30, 2021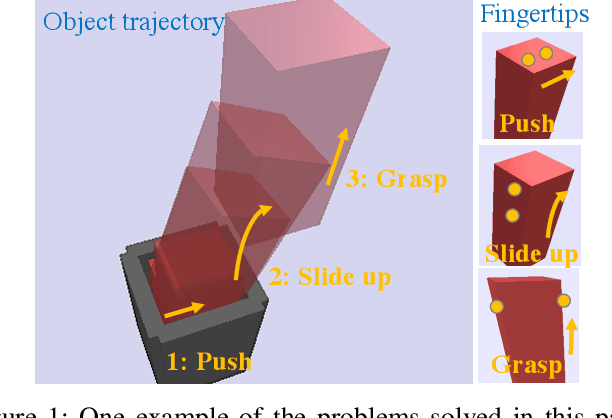


Within the field of robotic manipulation, a central goal is to replicate the human ability to manipulate any object in any situation using a sequence of manipulation primitives such as grasping, pushing, inserting, sliding, etc. Conceptually, each manipulation primitive restricts the object and robot to move on a lower-dimensional manifold defined by the primitive's dynamic equations of motion. Likewise, a manipulation sequence represents a dynamically feasible trajectory that traverses multiple manifolds. To manipulate any object in any situation, robotic systems must include the ability to automatically synthesize manipulation primitives (manifolds) and sequence those primitives into a coherent plan (find a path across the manifolds). This paper investigates a principled approach for solving dexterous manipulation planning. This approach is based on rapidly-exploring random trees which use contact modes to guide tree expansion along primitive manifolds. This paper extends this algorithm from 2D domains to 3D domains. We validated our algorithm on a large collection of simulated 3D manipulation tasks. These tasks required our algorithm to sequence between 6-42 manipulation primitives (i.e.\! distinct contact modes). We believe this work represents an important step towards robotic manipulation capabilities which generalize across objects and environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge