Broadband Beamforming via Linear Embedding
Paper and Code
Jun 14, 2022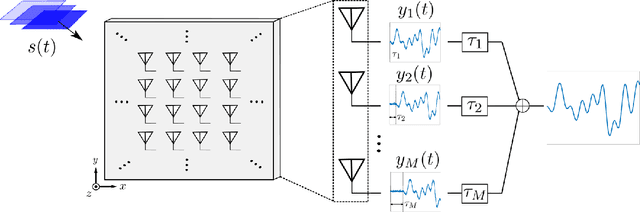
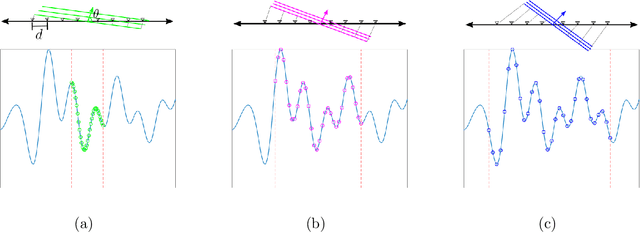
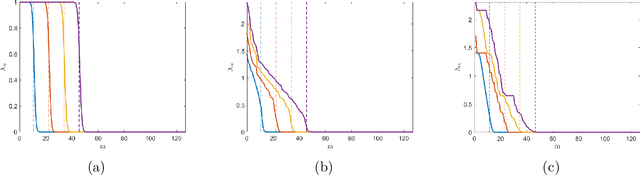
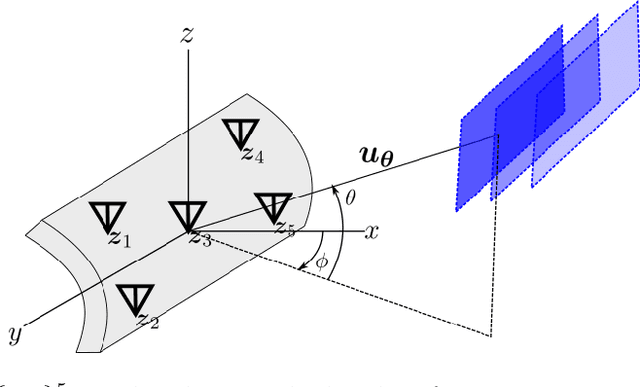
In modern applications multi-sensor arrays are subject to an ever-present demand to accommodate signals with higher bandwidths. Standard methods for broadband beamforming, namely digital beamforming and true-time delay, are difficult and expensive to implement at scale. In this work, we explore an alternative method of broadband beamforming that uses a set of linear measurements and a robust low-dimensional signal subspace model. The linear measurements, taken directly from the sensors, serve as a method for dimensionality reduction and serve to limit the array readout. From these embedded samples, we show how the original samples can be recovered to within a provably small residual error using a Slepian subspace model. Previous work in multi-sensor array subspace models have largely analyzed performance from a qualitative or asymptotic perspective. In contrast, we give quantitative estimates of how well different dimensionality reduction strategies preserve the array gain. We also show how spatial and temporal correlations can be used to relax the standard Nyquist sampling criterion, how recovery can be achieved through fast algorithms, and how "hardware friendly" linear measurements can be designed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge