A Hybrid Scattering Transform for Signals with Isolated Singularities
Paper and Code
Oct 10, 2021
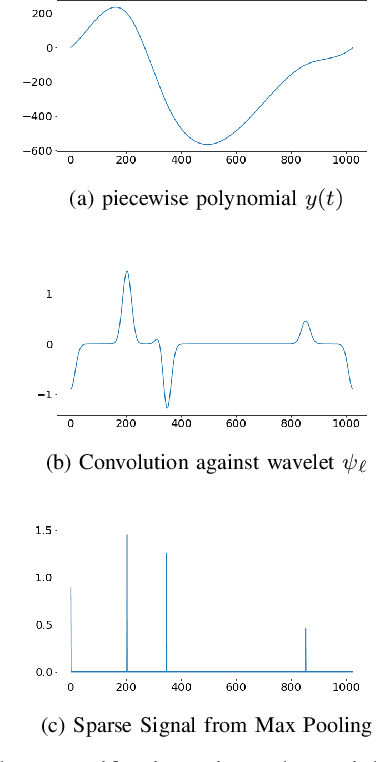
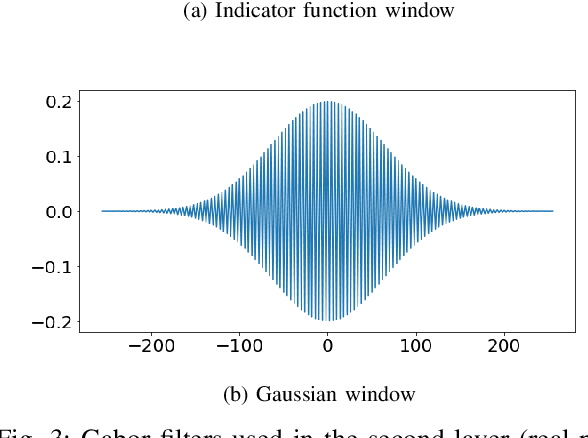
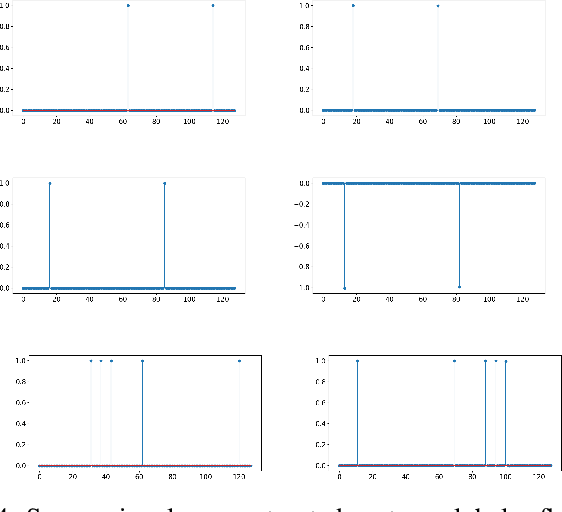
The scattering transform is a wavelet-based model of Convolutional Neural Networks originally introduced by S. Mallat. Mallat's analysis shows that this network has desirable stability and invariance guarantees and therefore helps explain the observation that the filters learned by early layers of a Convolutional Neural Network typically resemble wavelets. Our aim is to understand what sort of filters should be used in the later layers of the network. Towards this end, we propose a two-layer hybrid scattering transform. In our first layer, we convolve the input signal with a wavelet filter transform to promote sparsity, and, in the second layer, we convolve with a Gabor filter to leverage the sparsity created by the first layer. We show that these measurements characterize information about signals with isolated singularities. We also show that the Gabor measurements used in the second layer can be used to synthesize sparse signals such as those produced by the first layer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge