A Hybrid Scattering Transform for Signals with Isolated Singularities

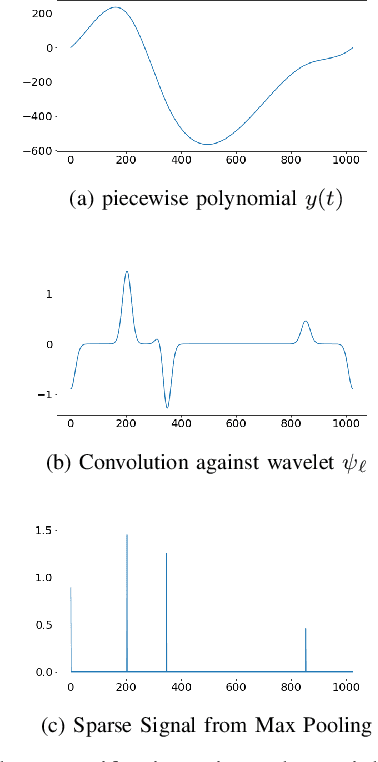
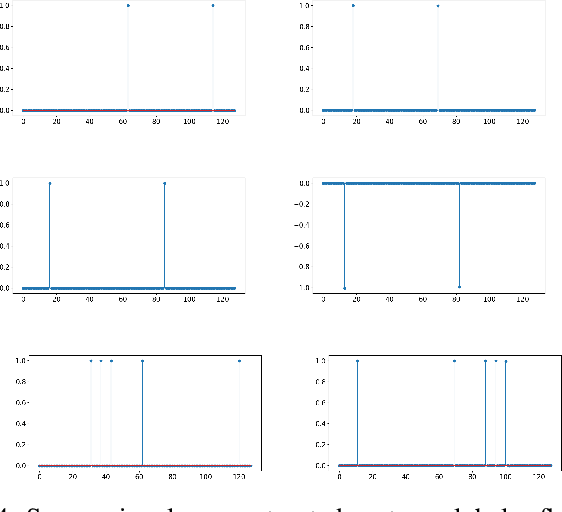
The scattering transform is a wavelet-based model of Convolutional Neural Networks originally introduced by S. Mallat. Mallat's analysis shows that this network has desirable stability and invariance guarantees and therefore helps explain the observation that the filters learned by early layers of a Convolutional Neural Network typically resemble wavelets. Our aim is to understand what sort of filters should be used in the later layers of the network. Towards this end, we propose a two-layer hybrid scattering transform. In our first layer, we convolve the input signal with a wavelet filter transform to promote sparsity, and, in the second layer, we convolve with a Gabor filter to leverage the sparsity created by the first layer. We show that these measurements characterize information about signals with isolated singularities. We also show that the Gabor measurements used in the second layer can be used to synthesize sparse signals such as those produced by the first layer.

Texture synthesis via projection onto multiscale, multilayer statistics

We provide a new model for texture synthesis based on a multiscale, multilayer feature extractor. Within the model, textures are represented by a set of statistics computed from ReLU wavelet coefficients at different layers, scales and orientations. A new image is synthesized by matching the target statistics via an iterative projection algorithm. We explain the necessity of the different types of pre-defined wavelet filters used in our model and the advantages of multilayer structures for image synthesis. We demonstrate the power of our model by generating samples of high quality textures and providing insights into deep representations for texture images.

Scattering Statistics of Generalized Spatial Poisson Point Processes

We present a machine learning model for the analysis of randomly generated discrete signals, which we model as the points of a homogeneous or inhomogeneous, compound Poisson point process. Like the wavelet scattering transform introduced by S. Mallat, our construction is a mathematical model of convolutional neural networks and is naturally invariant to translations and reflections. Our model replaces wavelets with Gabor-type measurements and therefore decouples the roles of scale and frequency. We show that, with suitably chosen nonlinearities, our measurements distinguish Poisson point processes from common self-similar processes, and separate different types of Poisson point processes based on the first and second moments of the arrival intensity $\lambda(t)$, as well as the absolute moments of the charges associated to each point.