Time-inhomogeneous diffusion geometry and topology

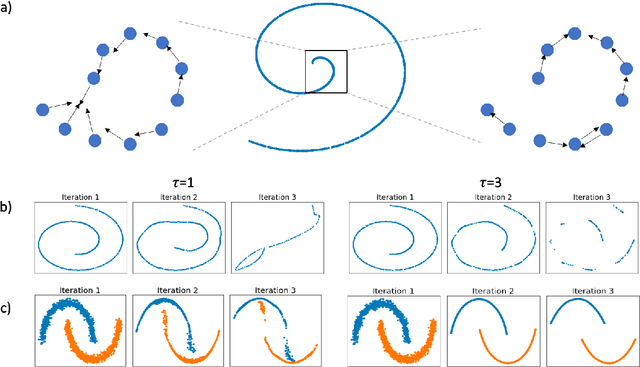
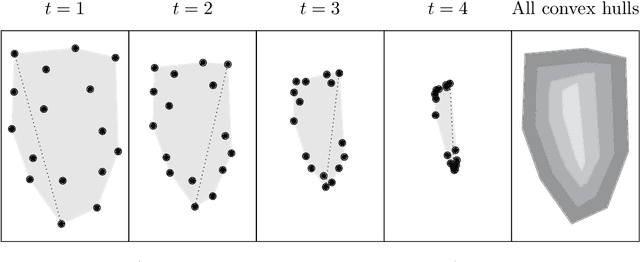
Diffusion condensation is a dynamic process that yields a sequence of multiscale data representations that aim to encode meaningful abstractions. It has proven effective for manifold learning, denoising, clustering, and visualization of high-dimensional data. Diffusion condensation is constructed as a time-inhomogeneous process where each step first computes and then applies a diffusion operator to the data. We theoretically analyze the convergence and evolution of this process from geometric, spectral, and topological perspectives. From a geometric perspective, we obtain convergence bounds based on the smallest transition probability and the radius of the data, whereas from a spectral perspective, our bounds are based on the eigenspectrum of the diffusion kernel. Our spectral results are of particular interest since most of the literature on data diffusion is focused on homogeneous processes. From a topological perspective, we show diffusion condensation generalizes centroid-based hierarchical clustering. We use this perspective to obtain a bound based on the number of data points, independent of their location. To understand the evolution of the data geometry beyond convergence, we use topological data analysis. We show that the condensation process itself defines an intrinsic diffusion homology. We use this intrinsic topology as well as an ambient topology to study how the data changes over diffusion time. We demonstrate both homologies in well-understood toy examples. Our work gives theoretical insights into the convergence of diffusion condensation, and shows that it provides a link between topological and geometric data analysis.

Learning shared neural manifolds from multi-subject FMRI data

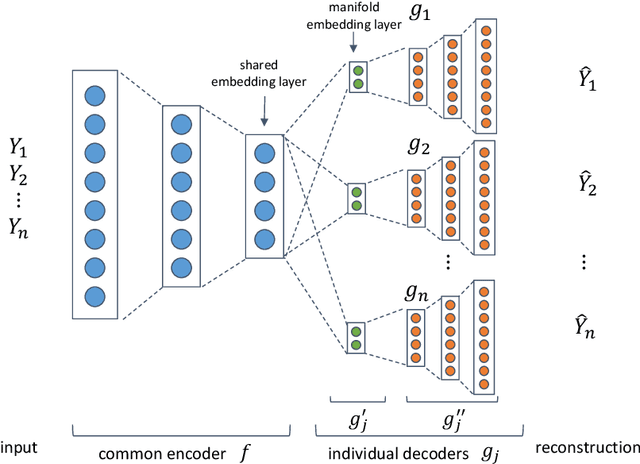
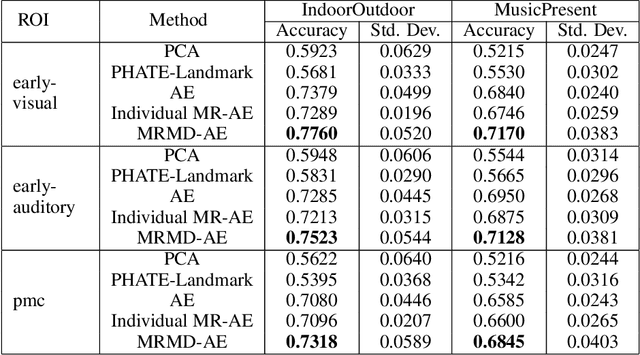
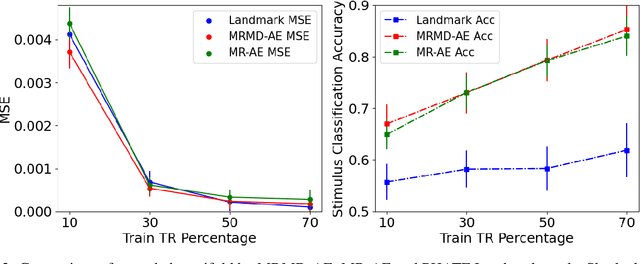
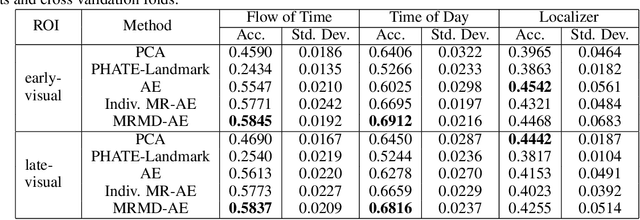
Functional magnetic resonance imaging (fMRI) is a notoriously noisy measurement of brain activity because of the large variations between individuals, signals marred by environmental differences during collection, and spatiotemporal averaging required by the measurement resolution. In addition, the data is extremely high dimensional, with the space of the activity typically having much lower intrinsic dimension. In order to understand the connection between stimuli of interest and brain activity, and analyze differences and commonalities between subjects, it becomes important to learn a meaningful embedding of the data that denoises, and reveals its intrinsic structure. Specifically, we assume that while noise varies significantly between individuals, true responses to stimuli will share common, low-dimensional features between subjects which are jointly discoverable. Similar approaches have been exploited previously but they have mainly used linear methods such as PCA and shared response modeling (SRM). In contrast, we propose a neural network called MRMD-AE (manifold-regularized multiple decoder, autoencoder), that learns a common embedding from multiple subjects in an experiment while retaining the ability to decode to individual raw fMRI signals. We show that our learned common space represents an extensible manifold (where new points not seen during training can be mapped), improves the classification accuracy of stimulus features of unseen timepoints, as well as improves cross-subject translation of fMRI signals. We believe this framework can be used for many downstream applications such as guided brain-computer interface (BCI) training in the future.

Visualizing High-Dimensional Trajectories on the Loss-Landscape of ANNs

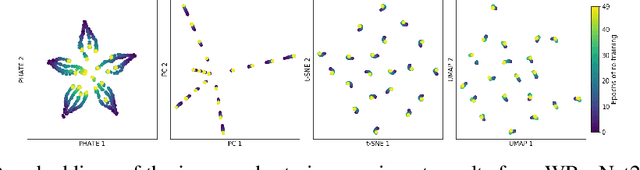
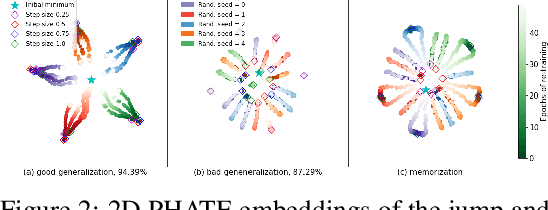
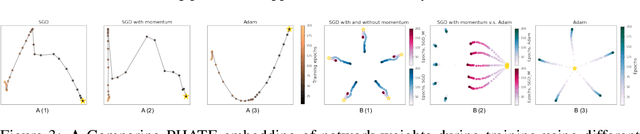
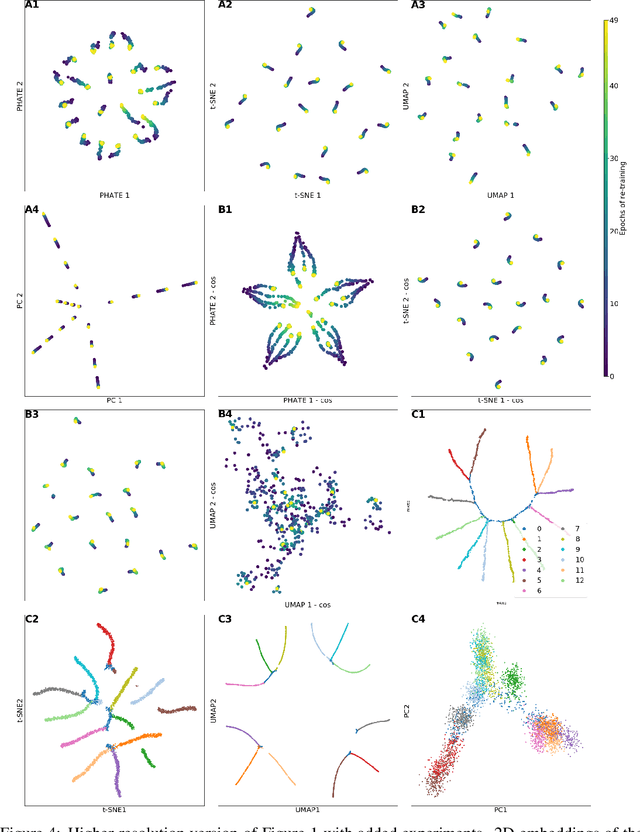
Training artificial neural networks requires the optimization of highly non-convex loss functions. Throughout the years, the scientific community has developed an extensive set of tools and architectures that render this optimization task tractable and a general intuition has been developed for choosing hyper parameters that help the models reach minima that generalize well to unseen data. However, for the most part, the difference in trainability in between architectures, tasks and even the gap in network generalization abilities still remain unexplained. Visualization tools have played a key role in uncovering key geometric characteristics of the loss-landscape of ANNs and how they impact trainability and generalization capabilities. However, most visualizations methods proposed so far have been relatively limited in their capabilities since they are of linear nature and only capture features in a limited number of dimensions. We propose the use of the modern dimensionality reduction method PHATE which represents the SOTA in terms of capturing both global and local structures of high-dimensional data. We apply this method to visualize the loss landscape during and after training. Our visualizations reveal differences in training trajectories and generalization capabilities when used to make comparisons between optimization methods, initializations, architectures, and datasets. Given this success we anticipate this method to be used in making informed choices about these aspects of neural networks.

TrajectoryNet: A Dynamic Optimal Transport Network for Modeling Cellular Dynamics

It is increasingly common to encounter data from dynamic processes captured by static cross-sectional measurements over time, particularly in biomedical settings. Recent attempts to model individual trajectories from this data use optimal transport to create pairwise matchings between time points. However, these methods cannot model continuous dynamics and non-linear paths that entities can take in these systems. To address this issue, we establish a link between continuous normalizing flows and dynamic optimal transport, that allows us to model the expected paths of points over time. Continuous normalizing flows are generally under constrained, as they are allowed to take an arbitrary path from the source to the target distribution. We present TrajectoryNet, which controls the continuous paths taken between distributions. We show how this is particularly applicable for studying cellular dynamics in data from single-cell RNA sequencing (scRNA-seq) technologies, and that TrajectoryNet improves upon recently proposed static optimal transport-based models that can be used for interpolating cellular distributions.

Learning Safe Policies with Expert Guidance

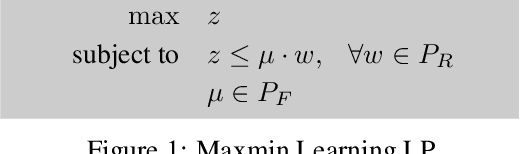
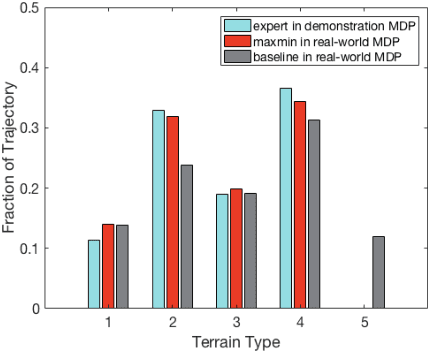
We propose a framework for ensuring safe behavior of a reinforcement learning agent when the reward function may be difficult to specify. In order to do this, we rely on the existence of demonstrations from expert policies, and we provide a theoretical framework for the agent to optimize in the space of rewards consistent with its existing knowledge. We propose two methods to solve the resulting optimization: an exact ellipsoid-based method and a method in the spirit of the "follow-the-perturbed-leader" algorithm. Our experiments demonstrate the behavior of our algorithm in both discrete and continuous problems. The trained agent safely avoids states with potential negative effects while imitating the behavior of the expert in the other states.