Learning shared neural manifolds from multi-subject FMRI data

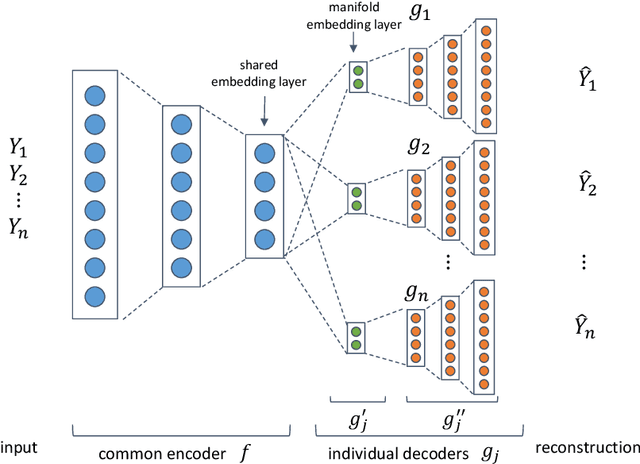
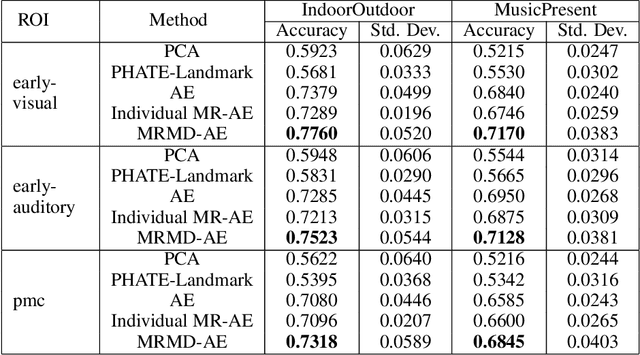
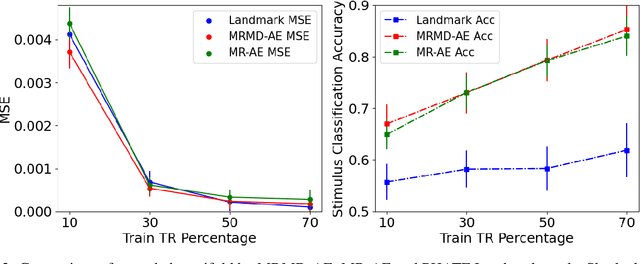
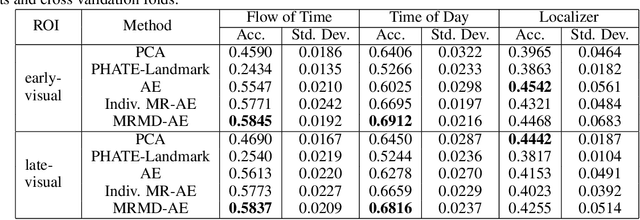
Functional magnetic resonance imaging (fMRI) is a notoriously noisy measurement of brain activity because of the large variations between individuals, signals marred by environmental differences during collection, and spatiotemporal averaging required by the measurement resolution. In addition, the data is extremely high dimensional, with the space of the activity typically having much lower intrinsic dimension. In order to understand the connection between stimuli of interest and brain activity, and analyze differences and commonalities between subjects, it becomes important to learn a meaningful embedding of the data that denoises, and reveals its intrinsic structure. Specifically, we assume that while noise varies significantly between individuals, true responses to stimuli will share common, low-dimensional features between subjects which are jointly discoverable. Similar approaches have been exploited previously but they have mainly used linear methods such as PCA and shared response modeling (SRM). In contrast, we propose a neural network called MRMD-AE (manifold-regularized multiple decoder, autoencoder), that learns a common embedding from multiple subjects in an experiment while retaining the ability to decode to individual raw fMRI signals. We show that our learned common space represents an extensible manifold (where new points not seen during training can be mapped), improves the classification accuracy of stimulus features of unseen timepoints, as well as improves cross-subject translation of fMRI signals. We believe this framework can be used for many downstream applications such as guided brain-computer interface (BCI) training in the future.

MURAL: An Unsupervised Random Forest-Based Embedding for Electronic Health Record Data

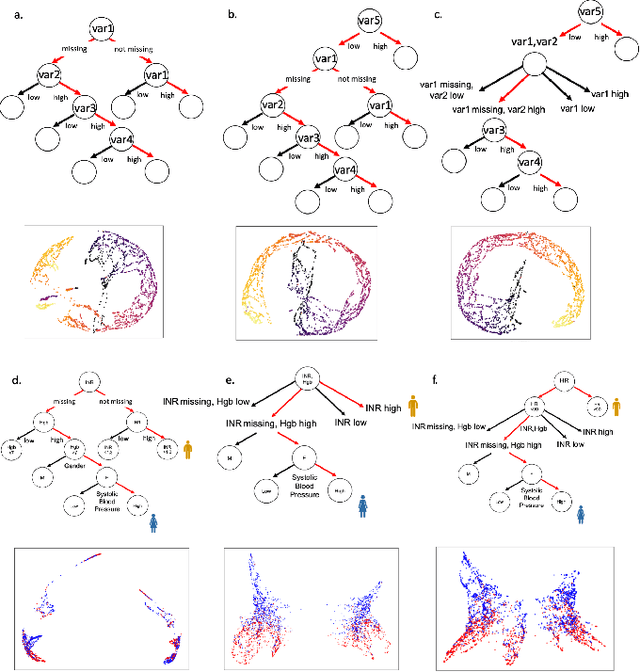
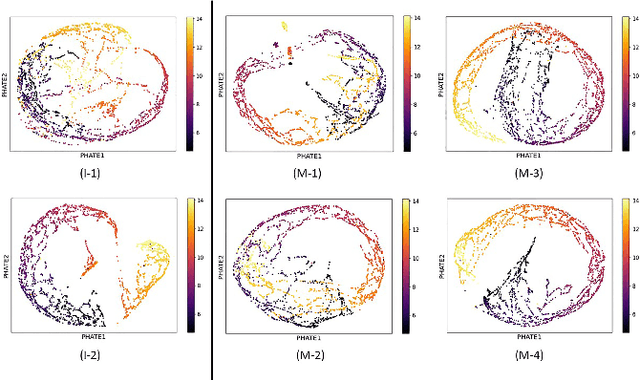
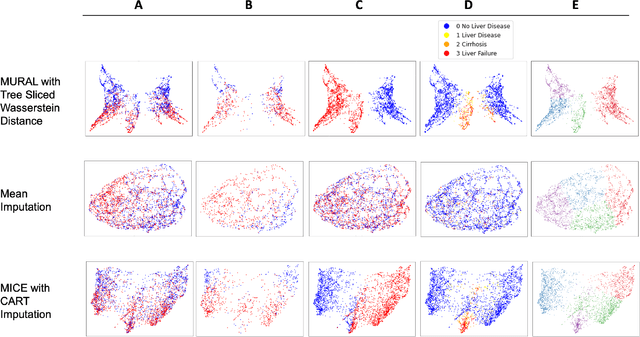
A major challenge in embedding or visualizing clinical patient data is the heterogeneity of variable types including continuous lab values, categorical diagnostic codes, as well as missing or incomplete data. In particular, in EHR data, some variables are {\em missing not at random (MNAR)} but deliberately not collected and thus are a source of information. For example, lab tests may be deemed necessary for some patients on the basis of suspected diagnosis, but not for others. Here we present the MURAL forest -- an unsupervised random forest for representing data with disparate variable types (e.g., categorical, continuous, MNAR). MURAL forests consist of a set of decision trees where node-splitting variables are chosen at random, such that the marginal entropy of all other variables is minimized by the split. This allows us to also split on MNAR variables and discrete variables in a way that is consistent with the continuous variables. The end goal is to learn the MURAL embedding of patients using average tree distances between those patients. These distances can be fed to nonlinear dimensionality reduction method like PHATE to derive visualizable embeddings. While such methods are ubiquitous in continuous-valued datasets (like single cell RNA-sequencing) they have not been used extensively in mixed variable data. We showcase the use of our method on one artificial and two clinical datasets. We show that using our approach, we can visualize and classify data more accurately than competing approaches. Finally, we show that MURAL can also be used to compare cohorts of patients via the recently proposed tree-sliced Wasserstein distances.