Structural Risk Minimization for $C^{1,1}$ Regression

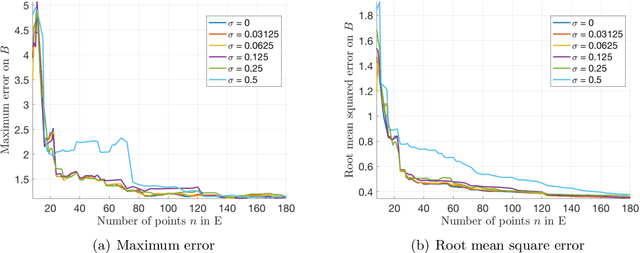
One means of fitting functions to high-dimensional data is by providing smoothness constraints. Recently, the following smooth function approximation problem was proposed: given a finite set $E \subset \mathbb{R}^d$ and a function $f: E \rightarrow \mathbb{R}$, interpolate the given information with a function $\widehat{f} \in \dot{C}^{1, 1}(\mathbb{R}^d)$ (the class of first-order differentiable functions with Lipschitz gradients) such that $\widehat{f}(a) = f(a)$ for all $a \in E$, and the value of $\mathrm{Lip}(\nabla \widehat{f})$ is minimal. An algorithm is provided that constructs such an approximating function $\widehat{f}$ and estimates the optimal Lipschitz constant $\mathrm{Lip}(\nabla \widehat{f})$ in the noiseless setting. We address statistical aspects of reconstructing the approximating function $\widehat{f}$ from a closely-related class $C^{1, 1}(\mathbb{R}^d)$ given samples from noisy data. We observe independent and identically distributed samples $y(a) = f(a) + \xi(a)$ for $a \in E$, where $\xi(a)$ is a noise term and the set $E \subset \mathbb{R}^d$ is fixed and known. We obtain uniform bounds relating the empirical risk and true risk over the class $\mathcal{F}_{\widetilde{M}} = \{f \in C^{1, 1}(\mathbb{R}^d) \mid \mathrm{Lip}(\nabla f) \leq \widetilde{M}\}$, where the quantity $\widetilde{M}$ grows with the number of samples at a rate governed by the metric entropy of the class $C^{1, 1}(\mathbb{R}^d)$. Finally, we provide an implementation using Vaidya's algorithm, supporting our results via numerical experiments on simulated data.

John's Walk

We present an affine-invariant random walk for drawing uniform random samples from a convex body $\mathcal{K} \subset \mathbb{R}^n$ for which the maximum volume inscribed ellipsoid, known as John's ellipsoid, may be computed. We consider a polytope $\mathcal{P} = \{x \in \mathbb{R}^n \mid Ax \leq 1\}$ where $A \in \mathbb{R}^{m \times n}$ as a special case. Our algorithm makes steps using uniform sampling from the John's ellipsoid of the symmetrization of $\mathcal{K}$ at the current point. We show that from a warm start, the random walk mixes in $\widetilde{O}(n^7)$ steps where the log factors depend only on constants determined by the warm start and error parameters (and not on the dimension or number of constraints defining the body). This sampling algorithm thus offers improvement over the affine-invariant Dikin Walk for polytopes (which mixes in $\widetilde{O}(mn)$ steps from a warm start) for applications in which $m \gg n$. Furthermore, we describe an $\widetilde{O}(mn^{\omega+1} + n^{2\omega+2})$ algorithm for finding a suitably approximate John's ellipsoid for a symmetric polytope based on Vaidya's algorithm, and show the mixing time is retained using these approximate ellipsoids (where $\omega < 2.373$ is the current value of the fast matrix multiplication constant).