A Robust Monotonic Single-Index Model for Skewed and Heavy-Tailed Data: A Deep Neural Network Approach Applied to Periodontal Studies

Periodontal pocket depth is a widely used biomarker for diagnosing risk of periodontal disease. However, pocket depth typically exhibits skewness and heavy-tailedness, and its relationship with clinical risk factors is often nonlinear. Motivated by periodontal studies, this paper develops a robust single-index modal regression framework for analyzing skewed and heavy-tailed data. Our method has the following novel features: (1) a flexible two-piece scale Student-$t$ error distribution that generalizes both normal and two-piece scale normal distributions; (2) a deep neural network with guaranteed monotonicity constraints to estimate the unknown single-index function; and (3) theoretical guarantees, including model identifiability and a universal approximation theorem. Our single-index model combines the flexibility of neural networks and the two-piece scale Student-$t$ distribution, delivering robust mode-based estimation that is resistant to outliers, while retaining clinical interpretability through parametric index coefficients. We demonstrate the performance of our method through simulation studies and an application to periodontal disease data from the HealthPartners Institute of Minnesota. The proposed methodology is implemented in the \textsf{R} package \href{https://doi.org/10.32614/CRAN.package.DNNSIM}{\textsc{DNNSIM}}.

Neural-g: A Deep Learning Framework for Mixing Density Estimation

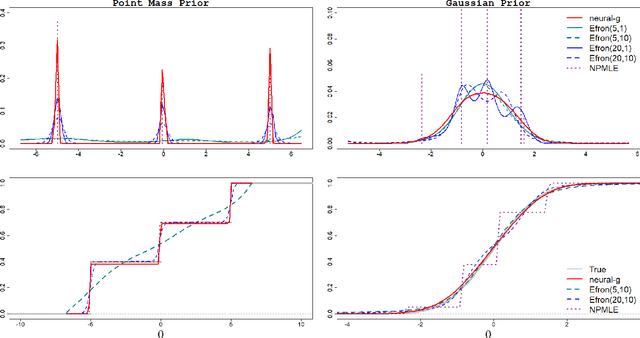
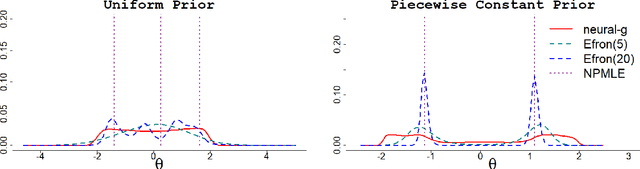
Mixing (or prior) density estimation is an important problem in machine learning and statistics, especially in empirical Bayes $g$-modeling where accurately estimating the prior is necessary for making good posterior inferences. In this paper, we propose neural-$g$, a new neural network-based estimator for $g$-modeling. Neural-$g$ uses a softmax output layer to ensure that the estimated prior is a valid probability density. Under default hyperparameters, we show that neural-$g$ is very flexible and capable of capturing many unknown densities, including those with flat regions, heavy tails, and/or discontinuities. In contrast, existing methods struggle to capture all of these prior shapes. We provide justification for neural-$g$ by establishing a new universal approximation theorem regarding the capability of neural networks to learn arbitrary probability mass functions. To accelerate convergence of our numerical implementation, we utilize a weighted average gradient descent approach to update the network parameters. Finally, we extend neural-$g$ to multivariate prior density estimation. We illustrate the efficacy of our approach through simulations and analyses of real datasets. A software package to implement neural-$g$ is publicly available at https://github.com/shijiew97/neuralG.

Sparse high-dimensional linear mixed modeling with a partitioned empirical Bayes ECM algorithm

High-dimensional longitudinal data is increasingly used in a wide range of scientific studies. However, there are few statistical methods for high-dimensional linear mixed models (LMMs), as most Bayesian variable selection or penalization methods are designed for independent observations. Additionally, the few available software packages for high-dimensional LMMs suffer from scalability issues. This work presents an efficient and accurate Bayesian framework for high-dimensional LMMs. We use empirical Bayes estimators of hyperparameters for increased flexibility and an Expectation-Conditional-Minimization (ECM) algorithm for computationally efficient maximum a posteriori probability (MAP) estimation of parameters. The novelty of the approach lies in its partitioning and parameter expansion as well as its fast and scalable computation. We illustrate Linear Mixed Modeling with PaRtitiOned empirical Bayes ECM (LMM-PROBE) in simulation studies evaluating fixed and random effects estimation along with computation time. A real-world example is provided using data from a study of lupus in children, where we identify genes and clinical factors associated with a new lupus biomarker and predict the biomarker over time.

Heteroscedastic sparse high-dimensional linear regression with a partitioned empirical Bayes ECM algorithm

Sparse linear regression methods for high-dimensional data often assume that residuals have constant variance. When this assumption is violated, it can lead to bias in estimated coefficients, prediction intervals (PI) with improper length, and increased type I errors. We propose a heteroscedastic high-dimensional linear regression model through a partitioned empirical Bayes Expectation Conditional Maximization (H-PROBE) algorithm. H-PROBE is a computationally efficient maximum a posteriori estimation approach based on a Parameter-Expanded Expectation-Conditional-Maximization algorithm. It requires minimal prior assumptions on the regression parameters through plug-in empirical Bayes estimates of hyperparameters. The variance model uses a multivariate log-Gamma prior on coefficients that can incorporate covariates hypothesized to impact heterogeneity. The motivation of our approach is a study relating Aphasia Quotient (AQ) to high-resolution T2 neuroimages of brain damage in stroke patients. AQ is a vital measure of language impairment and informs treatment decisions, but it is challenging to measure and subject to heteroscedastic errors. It is, therefore, of clinical importance -- and the goal of this paper -- to use high-dimensional neuroimages to predict and provide PIs for AQ that accurately reflect the heterogeneity in residual variance. Our analysis demonstrates that H-PROBE can use markers of heterogeneity to provide narrower PI widths than standard methods without sacrificing coverage. Through extensive simulation studies, we exhibit that H-PROBE results in superior prediction, variable selection, and predictive inference than competing methods.