A Simulation-Free Deep Learning Approach to Stochastic Optimal Control
Paper and Code
Oct 07, 2024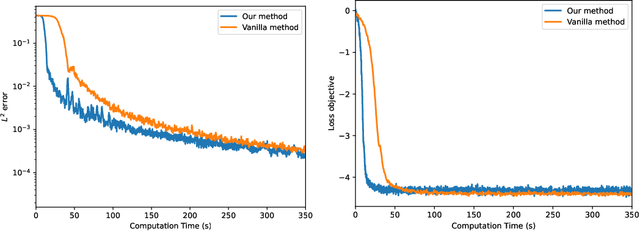

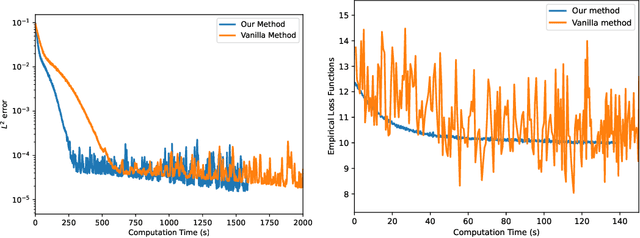

We propose a simulation-free algorithm for the solution of generic problems in stochastic optimal control (SOC). Unlike existing methods, our approach does not require the solution of an adjoint problem, but rather leverages Girsanov theorem to directly calculate the gradient of the SOC objective on-policy. This allows us to speed up the optimization of control policies parameterized by neural networks since it completely avoids the expensive back-propagation step through stochastic differential equations (SDEs) used in the Neural SDE framework. In particular, it enables us to solve SOC problems in high dimension and on long time horizons. We demonstrate the efficiency of our approach in various domains of applications, including standard stochastic optimal control problems, sampling from unnormalized distributions via construction of a Schr\"odinger-F\"ollmer process, and fine-tuning of pre-trained diffusion models. In all cases our method is shown to outperform the existing methods in both the computing time and memory efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge