Asymptotics of Learning with Deep Structured (Random) Features

For a large class of feature maps we provide a tight asymptotic characterisation of the test error associated with learning the readout layer, in the high-dimensional limit where the input dimension, hidden layer widths, and number of training samples are proportionally large. This characterization is formulated in terms of the population covariance of the features. Our work is partially motivated by the problem of learning with Gaussian rainbow neural networks, namely deep non-linear fully-connected networks with random but structured weights, whose row-wise covariances are further allowed to depend on the weights of previous layers. For such networks we also derive a closed-form formula for the feature covariance in terms of the weight matrices. We further find that in some cases our results can capture feature maps learned by deep, finite-width neural networks trained under gradient descent.

Deterministic equivalent and error universality of deep random features learning

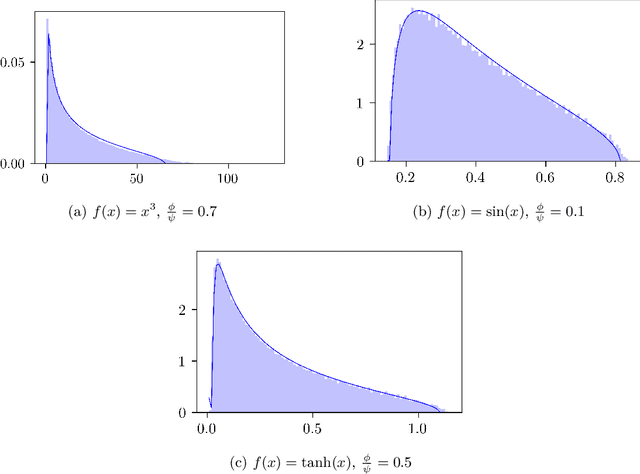
This manuscript considers the problem of learning a random Gaussian network function using a fully connected network with frozen intermediate layers and trainable readout layer. This problem can be seen as a natural generalization of the widely studied random features model to deeper architectures. First, we prove Gaussian universality of the test error in a ridge regression setting where the learner and target networks share the same intermediate layers, and provide a sharp asymptotic formula for it. Establishing this result requires proving a deterministic equivalent for traces of the deep random features sample covariance matrices which can be of independent interest. Second, we conjecture the asymptotic Gaussian universality of the test error in the more general setting of arbitrary convex losses and generic learner/target architectures. We provide extensive numerical evidence for this conjecture, which requires the derivation of closed-form expressions for the layer-wise post-activation population covariances. In light of our results, we investigate the interplay between architecture design and implicit regularization.

Chaining of Numerical Black-box Algorithms: Warm-Starting and Switching Points

Dynamic algorithm selection can be beneficial for solving numerical black-box problems, in which we implement an online switching mechanism between optimization algorithms. In this approach, we need to decide when a switch should take place and which algorithm to pick for the switching. Intuitively, this approach chains the algorithms for combining the well-performing segments from the performance profile of the algorithms. To realize efficient chaining, we investigate two important aspects - how the switching point influences the overall performance and how to warm-start an algorithm with information stored in its predecessor. To delve into those aspects, we manually construct a portfolio comprising five state-of-the-art optimization algorithms and only consider a single switch between each algorithm pair. After benchmarking those algorithms with the BBOB problem set, we choose the switching point for each pair by maximizing the theoretical performance gain. The theoretical gain is compared to the actual gain obtained by executing the switching procedure with the corresponding switching point. Moreover, we devise algorithm-specific warm-starting methods for initializing the algorithm after the switching with the information learned from its predecessor. Our empirical results show that on some BBOB problems, the theoretical gain is realized or even surpassed by the actual gain. More importantly, this approach discovers a chain that outperforms the single best algorithm on many problem instances. Also, we show that a proper warm-starting procedure is crucial to achieving high actual performance gain for some algorithm pairs. Lastly, with a sensitivity analysis, we find the actual performance gain is hugely affected by the switching point, and in some cases, the switching point yielding the best actual performance differs from the one computed from the theoretical gain.

Analysis of One-Hidden-Layer Neural Networks via the Resolvent Method

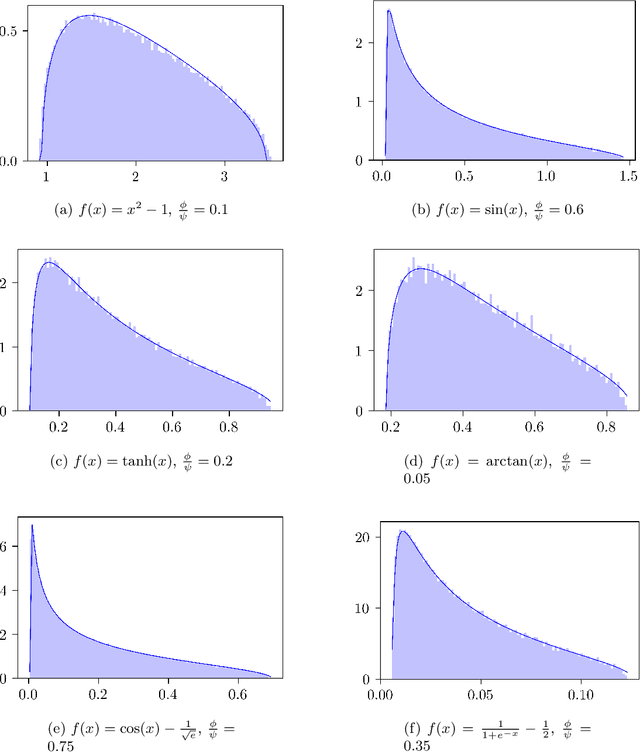
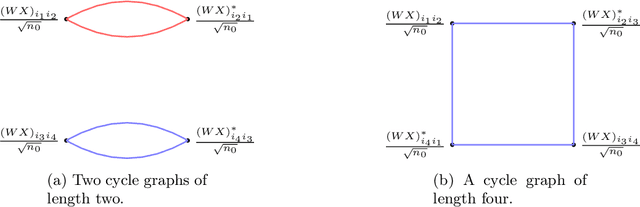
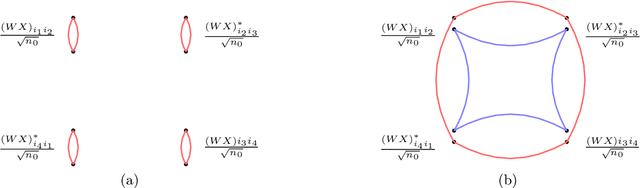
We compute the asymptotic empirical spectral distribution of a non-linear random matrix model by using the resolvent method. Motivated by random neural networks, we consider the random matrix $M = Y Y^\ast$ with $Y = f(WX)$, where $W$ and $X$ are random rectangular matrices with i.i.d. centred entries and $f$ is a non-linear smooth function which is applied entry-wise. We prove that the Stieltjes transform of the limiting spectral distribution satisfies a quartic self-consistent equation up to some error terms, which is exactly the equation obtained by [Pennington, Worah] and [Benigni, P\'{e}ch\'{e}] with the moment method approach. In addition, we extend the previous results to the case of additive bias $Y=f(WX+B)$ with $B$ being an independent rank-one Gaussian random matrix, closer modelling the neural network infrastructures encountering in practice. Our approach following the \emph{resolvent method} is more robust than the moment method and is expected to provide insights also for models where the combinatorics of the latter become intractable.