Permutation recovery of spikes in noisy high-dimensional tensor estimation

We study the dynamics of gradient flow in high dimensions for the multi-spiked tensor problem, where the goal is to estimate $r$ unknown signal vectors (spikes) from noisy Gaussian tensor observations. Specifically, we analyze the maximum likelihood estimation procedure, which involves optimizing a highly nonconvex random function. We determine the sample complexity required for gradient flow to efficiently recover all spikes, without imposing any assumptions on the separation of the signal-to-noise ratios (SNRs). More precisely, our results provide the sample complexity required to guarantee recovery of the spikes up to a permutation. Our work builds on our companion paper [Ben Arous, Gerbelot, Piccolo 2024], which studies Langevin dynamics and determines the sample complexity and separation conditions for the SNRs necessary for ensuring exact recovery of the spikes (where the recovered permutation matches the identity). During the recovery process, the correlations between the estimators and the hidden vectors increase in a sequential manner. The order in which these correlations become significant depends on their initial values and the corresponding SNRs, which ultimately determines the permutation of the recovered spikes.

Stochastic gradient descent in high dimensions for multi-spiked tensor PCA

We study the dynamics in high dimensions of online stochastic gradient descent for the multi-spiked tensor model. This multi-index model arises from the tensor principal component analysis (PCA) problem with multiple spikes, where the goal is to estimate $r$ unknown signal vectors within the $N$-dimensional unit sphere through maximum likelihood estimation from noisy observations of a $p$-tensor. We determine the number of samples and the conditions on the signal-to-noise ratios (SNRs) required to efficiently recover the unknown spikes from natural random initializations. We show that full recovery of all spikes is possible provided a number of sample scaling as $N^{p-2}$, matching the algorithmic threshold identified in the rank-one case [Ben Arous, Gheissari, Jagannath 2020, 2021]. Our results are obtained through a detailed analysis of a low-dimensional system that describes the evolution of the correlations between the estimators and the spikes, while controlling the noise in the dynamics. We find that the spikes are recovered sequentially in a process we term "sequential elimination": once a correlation exceeds a critical threshold, all correlations sharing a row or column index become sufficiently small, allowing the next correlation to grow and become macroscopic. The order in which correlations become macroscopic depends on their initial values and the corresponding SNRs, leading to either exact recovery or recovery of a permutation of the spikes. In the matrix case, when $p=2$, if the SNRs are sufficiently separated, we achieve exact recovery of the spikes, whereas equal SNRs lead to recovery of the subspace spanned by the spikes.

High-dimensional optimization for multi-spiked tensor PCA

We study the dynamics of two local optimization algorithms, online stochastic gradient descent (SGD) and gradient flow, within the framework of the multi-spiked tensor model in the high-dimensional regime. This multi-index model arises from the tensor principal component analysis (PCA) problem, which aims to infer $r$ unknown, orthogonal signal vectors within the $N$-dimensional unit sphere through maximum likelihood estimation from noisy observations of an order-$p$ tensor. We determine the number of samples and the conditions on the signal-to-noise ratios (SNRs) required to efficiently recover the unknown spikes from natural initializations. Specifically, we distinguish between three types of recovery: exact recovery of each spike, recovery of a permutation of all spikes, and recovery of the correct subspace spanned by the signal vectors. We show that with online SGD, it is possible to recover all spikes provided a number of sample scaling as $N^{p-2}$, aligning with the computational threshold identified in the rank-one tensor PCA problem [Ben Arous, Gheissari, Jagannath 2020, 2021]. For gradient flow, we show that the algorithmic threshold to efficiently recover the first spike is also of order $N^{p-2}$. However, recovering the subsequent directions requires the number of samples to scale as $N^{p-1}$. Our results are obtained through a detailed analysis of a low-dimensional system that describes the evolution of the correlations between the estimators and the spikes. In particular, the hidden vectors are recovered one by one according to a sequential elimination phenomenon: as one correlation exceeds a critical threshold, all correlations sharing a row or column index decrease and become negligible, allowing the subsequent correlation to grow and become macroscopic. The sequence in which correlations become macroscopic depends on their initial values and on the associated SNRs.

Topological complexity of spiked random polynomials and finite-rank spherical integrals

We study the annealed complexity of a random Gaussian homogeneous polynomial on the $N$-dimensional unit sphere in the presence of deterministic polynomials that depend on fixed unit vectors and external parameters. In particular, we establish variational formulas for the exponential asymptotics of the average number of total critical points and of local maxima. This is obtained through the Kac-Rice formula and the determinant asymptotics of a finite-rank perturbation of a Gaussian Wigner matrix. More precisely, the determinant analysis is based on recent advances on finite-rank spherical integrals by [Guionnet, Husson 2022] to study the large deviations of multi-rank spiked Gaussian Wigner matrices. The analysis of the variational problem identifies a topological phase transition. There is an exact threshold for the external parameters such that, once exceeded, the complexity function vanishes into new regions in which the critical points are close to the given vectors. Interestingly, these regions also include those where critical points are close to multiple vectors.

Analysis of One-Hidden-Layer Neural Networks via the Resolvent Method

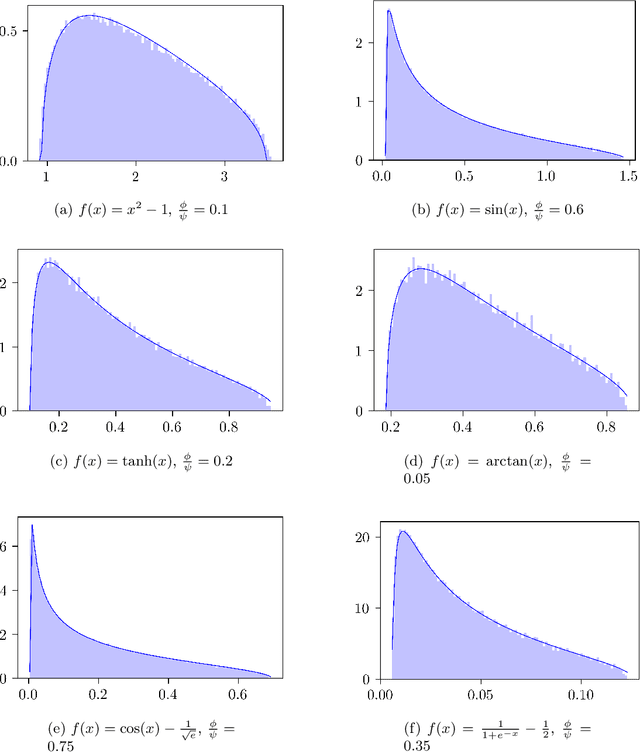
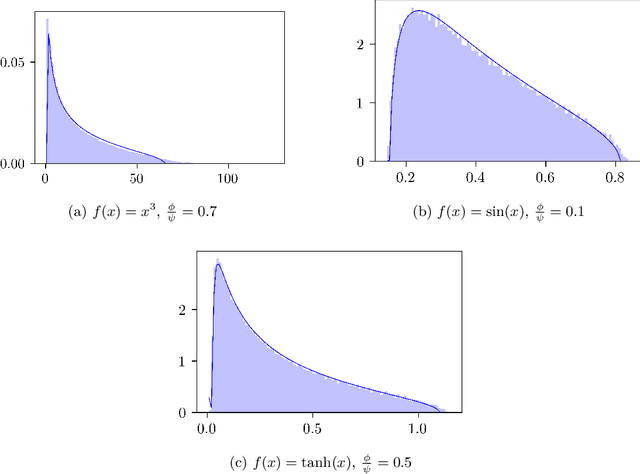
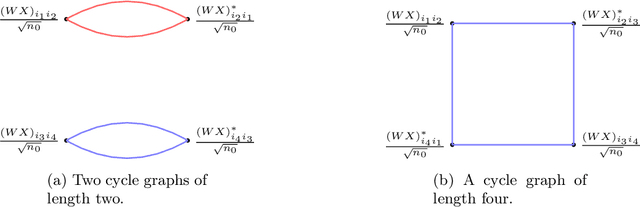
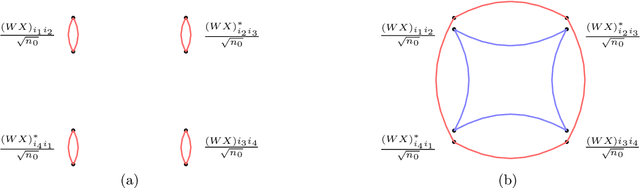
We compute the asymptotic empirical spectral distribution of a non-linear random matrix model by using the resolvent method. Motivated by random neural networks, we consider the random matrix $M = Y Y^\ast$ with $Y = f(WX)$, where $W$ and $X$ are random rectangular matrices with i.i.d. centred entries and $f$ is a non-linear smooth function which is applied entry-wise. We prove that the Stieltjes transform of the limiting spectral distribution satisfies a quartic self-consistent equation up to some error terms, which is exactly the equation obtained by [Pennington, Worah] and [Benigni, P\'{e}ch\'{e}] with the moment method approach. In addition, we extend the previous results to the case of additive bias $Y=f(WX+B)$ with $B$ being an independent rank-one Gaussian random matrix, closer modelling the neural network infrastructures encountering in practice. Our approach following the \emph{resolvent method} is more robust than the moment method and is expected to provide insights also for models where the combinatorics of the latter become intractable.