Analysis of One-Hidden-Layer Neural Networks via the Resolvent Method
Paper and Code
May 11, 2021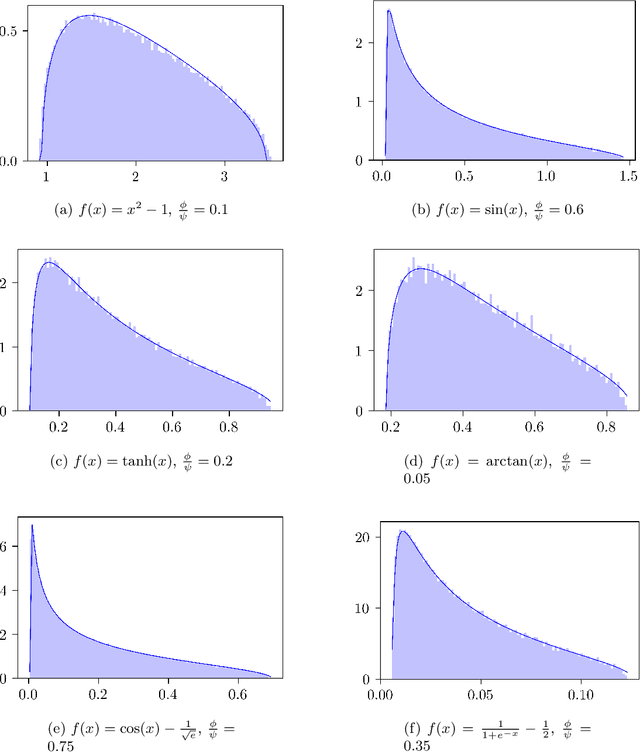
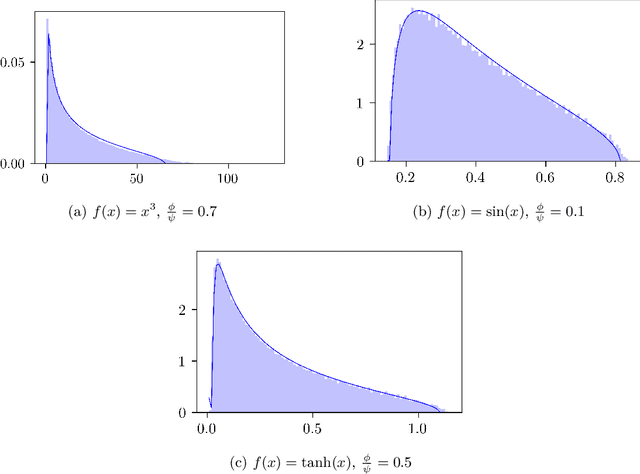
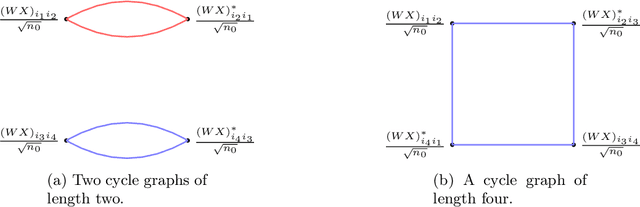
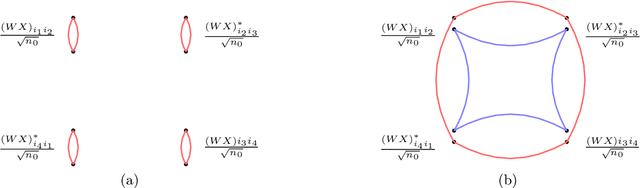
We compute the asymptotic empirical spectral distribution of a non-linear random matrix model by using the resolvent method. Motivated by random neural networks, we consider the random matrix $M = Y Y^\ast$ with $Y = f(WX)$, where $W$ and $X$ are random rectangular matrices with i.i.d. centred entries and $f$ is a non-linear smooth function which is applied entry-wise. We prove that the Stieltjes transform of the limiting spectral distribution satisfies a quartic self-consistent equation up to some error terms, which is exactly the equation obtained by [Pennington, Worah] and [Benigni, P\'{e}ch\'{e}] with the moment method approach. In addition, we extend the previous results to the case of additive bias $Y=f(WX+B)$ with $B$ being an independent rank-one Gaussian random matrix, closer modelling the neural network infrastructures encountering in practice. Our approach following the \emph{resolvent method} is more robust than the moment method and is expected to provide insights also for models where the combinatorics of the latter become intractable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge