Robust Utility Optimization via a GAN Approach

Robust utility optimization enables an investor to deal with market uncertainty in a structured way, with the goal of maximizing the worst-case outcome. In this work, we propose a generative adversarial network (GAN) approach to (approximately) solve robust utility optimization problems in general and realistic settings. In particular, we model both the investor and the market by neural networks (NN) and train them in a mini-max zero-sum game. This approach is applicable for any continuous utility function and in realistic market settings with trading costs, where only observable information of the market can be used. A large empirical study shows the versatile usability of our method. Whenever an optimal reference strategy is available, our method performs on par with it and in the (many) settings without known optimal strategy, our method outperforms all other reference strategies. Moreover, we can conclude from our study that the trained path-dependent strategies do not outperform Markovian ones. Lastly, we uncover that our generative approach for learning optimal, (non-) robust investments under trading costs generates universally applicable alternatives to well known asymptotic strategies of idealized settings.

How (Implicit) Regularization of ReLU Neural Networks Characterizes the Learned Function -- Part II: the Multi-D Case of Two Layers with Random First Layer

Randomized neural networks (randomized NNs), where only the terminal layer's weights are optimized constitute a powerful model class to reduce computational time in training the neural network model. At the same time, these models generalize surprisingly well in various regression and classification tasks. In this paper, we give an exact macroscopic characterization (i.e., a characterization in function space) of the generalization behavior of randomized, shallow NNs with ReLU activation (RSNs). We show that RSNs correspond to a generalized additive model (GAM)-typed regression in which infinitely many directions are considered: the infinite generalized additive model (IGAM). The IGAM is formalized as solution to an optimization problem in function space for a specific regularization functional and a fairly general loss. This work is an extension to multivariate NNs of prior work, where we showed how wide RSNs with ReLU activation behave like spline regression under certain conditions and if the input is one-dimensional.

Infinite width (finite depth) neural networks benefit from multi-task learning unlike shallow Gaussian Processes -- an exact quantitative macroscopic characterization

We prove in this paper that optimizing wide ReLU neural networks (NNs) with at least one hidden layer using l2-regularization on the parameters enforces multi-task learning due to representation-learning - also in the limit of width to infinity. This is in contrast to multiple other results in the literature, in which idealized settings are assumed and where wide (ReLU)-NNs loose their ability to benefit from multi-task learning in the infinite width limit. We deduce the ability of multi-task learning from proving an exact quantitative macroscopic characterization of the learned NN in an appropriate function space.

NOMU: Neural Optimization-based Model Uncertainty

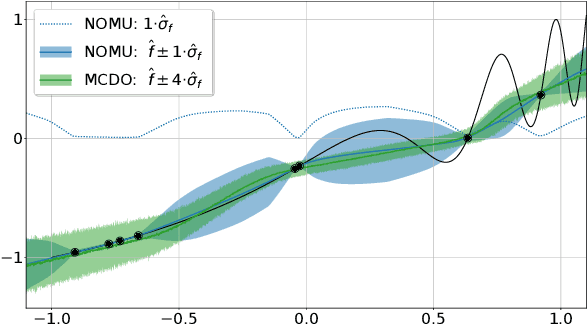
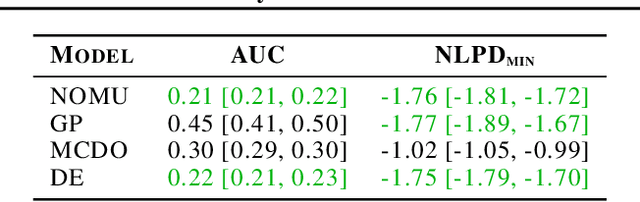
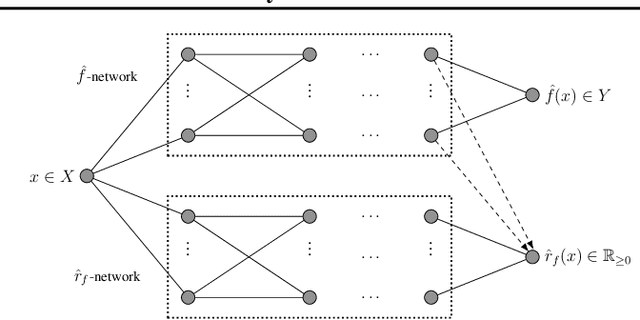
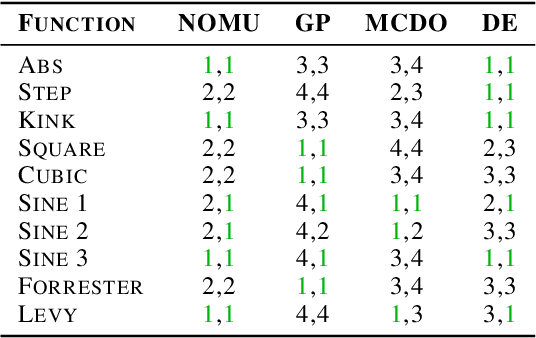
We introduce a new approach for capturing model uncertainty for neural networks (NNs) in regression, which we call Neural Optimization-based Model Uncertainty (NOMU). The main idea of NOMU is to design a network architecture consisting of two connected sub-networks, one for the model prediction and one for the model uncertainty, and to train it using a carefully designed loss function. With this design, NOMU can provide model uncertainty for any given (previously trained) NN by plugging it into the framework as the sub-network used for model prediction. NOMU is designed to yield uncertainty bounds (UBs) that satisfy four important desiderata regarding model uncertainty, which established methods often do not satisfy. Furthermore, our UBs are themselves representable as a single NN, which leads to computational cost advantages in applications such as Bayesian optimization. We evaluate NOMU experimentally in multiple settings. For regression, we show that NOMU performs as well as or better than established benchmarks. For Bayesian optimization, we show that NOMU outperforms all other benchmarks.

How implicit regularization of Neural Networks affects the learned function -- Part I

Today, various forms of neural networks are trained to perform approximation tasks in many fields. However, the solutions obtained are not wholly understood. Empirical results suggest that the training favors regularized solutions. These observations motivate us to analyze properties of the solutions found by the gradient descent algorithm frequently employed to perform the training task. As a starting point, we consider one dimensional (shallow) neural networks in which weights are chosen randomly and only the terminal layer is trained. We show, that the resulting solution converges to the smooth spline interpolation of the training data as the number of hidden nodes tends to infinity. This might give valuable insight on the properties of the solutions obtained using gradient descent methods in general settings.