JUCAL: Jointly Calibrating Aleatoric and Epistemic Uncertainty in Classification Tasks

We study post-calibration uncertainty for trained ensembles of classifiers. Specifically, we consider both aleatoric (label noise) and epistemic (model) uncertainty. Among the most popular and widely used calibration methods in classification are temperature scaling (i.e., pool-then-calibrate) and conformal methods. However, the main shortcoming of these calibration methods is that they do not balance the proportion of aleatoric and epistemic uncertainty. Not balancing these uncertainties can severely misrepresent predictive uncertainty, leading to overconfident predictions in some input regions while being underconfident in others. To address this shortcoming, we present a simple but powerful calibration algorithm Joint Uncertainty Calibration (JUCAL) that jointly calibrates aleatoric and epistemic uncertainty. JUCAL jointly calibrates two constants to weight and scale epistemic and aleatoric uncertainties by optimizing the negative log-likelihood (NLL) on the validation/calibration dataset. JUCAL can be applied to any trained ensemble of classifiers (e.g., transformers, CNNs, or tree-based methods), with minimal computational overhead, without requiring access to the models' internal parameters. We experimentally evaluate JUCAL on various text classification tasks, for ensembles of varying sizes and with different ensembling strategies. Our experiments show that JUCAL significantly outperforms SOTA calibration methods across all considered classification tasks, reducing NLL and predictive set size by up to 15% and 20%, respectively. Interestingly, even applying JUCAL to an ensemble of size 5 can outperform temperature-scaled ensembles of size up to 50 in terms of NLL and predictive set size, resulting in up to 10 times smaller inference costs. Thus, we propose JUCAL as a new go-to method for calibrating ensembles in classification.

Nonparametric Filtering, Estimation and Classification using Neural Jump ODEs

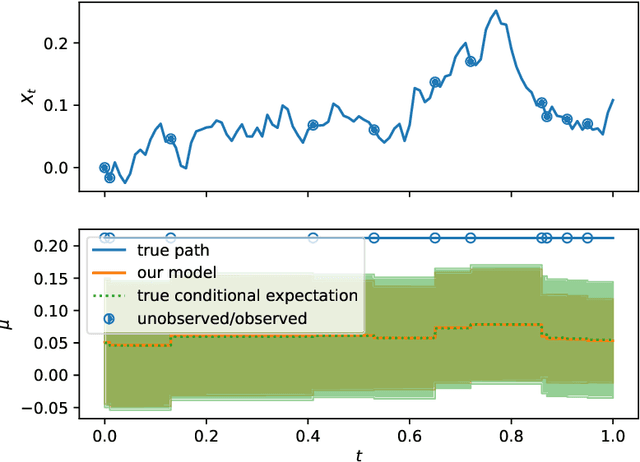
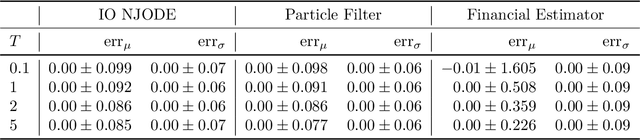
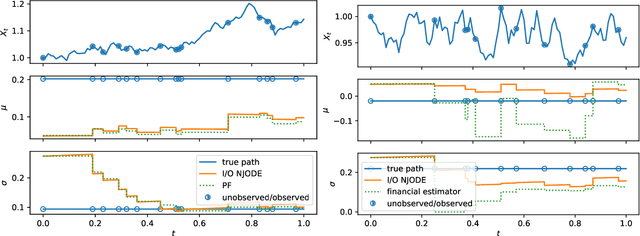
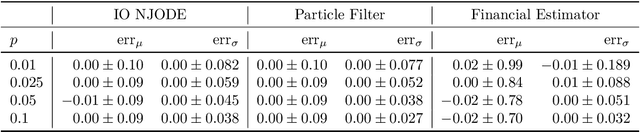
Neural Jump ODEs model the conditional expectation between observations by neural ODEs and jump at arrival of new observations. They have demonstrated effectiveness for fully data-driven online forecasting in settings with irregular and partial observations, operating under weak regularity assumptions. This work extends the framework to input-output systems, enabling direct applications in online filtering and classification. We establish theoretical convergence guarantees for this approach, providing a robust solution to $L^2$-optimal filtering. Empirical experiments highlight the model's superior performance over classical parametric methods, particularly in scenarios with complex underlying distributions. These results emphasise the approach's potential in time-sensitive domains such as finance and health monitoring, where real-time accuracy is crucial.

Prices, Bids, Values: Everything, Everywhere, All at Once

We study the design of iterative combinatorial auctions (ICAs). The main challenge in this domain is that the bundle space grows exponentially in the number of items. To address this, several papers have recently proposed machine learning (ML)-based preference elicitation algorithms that aim to elicit only the most important information from bidders to maximize efficiency. The SOTA ML-based algorithms elicit bidders' preferences via value queries (i.e., "What is your value for the bundle $\{A,B\}$?"). However, the most popular iterative combinatorial auction in practice elicits information via more practical \emph{demand queries} (i.e., "At prices $p$, what is your most preferred bundle of items?"). In this paper, we examine the advantages of value and demand queries from both an auction design and an ML perspective. We propose a novel ML algorithm that provably integrates the full information from both query types. As suggested by our theoretical analysis, our experimental results verify that combining demand and value queries results in significantly better learning performance. Building on these insights, we present MLHCA, the most efficient ICA ever designed. MLHCA substantially outperforms the previous SOTA in realistic auction settings, delivering large efficiency gains. Compared to the previous SOTA, MLHCA reduces efficiency loss by up to a factor of 10, and in the most challenging and realistic domain, MLHCA outperforms the previous SOTA using 30% fewer queries. Thus, MLHCA achieves efficiency improvements that translate to welfare gains of hundreds of millions of USD, while also reducing the cognitive load on the bidders, establishing a new benchmark both for practicability and for economic impact.

Machine Learning-powered Combinatorial Clock Auction

We study the design of iterative combinatorial auctions (ICAs). The main challenge in this domain is that the bundle space grows exponentially in the number of items. To address this, several papers have recently proposed machine learning (ML)-based preference elicitation algorithms that aim to elicit only the most important information from bidders. However, from a practical point of view, the main shortcoming of this prior work is that those designs elicit bidders' preferences via value queries (i.e., ``What is your value for the bundle $\{A,B\}$?''). In most real-world ICA domains, value queries are considered impractical, since they impose an unrealistically high cognitive burden on bidders, which is why they are not used in practice. In this paper, we address this shortcoming by designing an ML-powered combinatorial clock auction that elicits information from the bidders only via demand queries (i.e., ``At prices $p$, what is your most preferred bundle of items?''). We make two key technical contributions: First, we present a novel method for training an ML model on demand queries. Second, based on those trained ML models, we introduce an efficient method for determining the demand query with the highest clearing potential, for which we also provide a theoretical foundation. We experimentally evaluate our ML-based demand query mechanism in several spectrum auction domains and compare it against the most established real-world ICA: the combinatorial clock auction (CCA). Our mechanism significantly outperforms the CCA in terms of efficiency in all domains, it achieves higher efficiency in a significantly reduced number of rounds, and, using linear prices, it exhibits vastly higher clearing potential. Thus, with this paper we bridge the gap between research and practice and propose the first practical ML-powered ICA.

Extending Path-Dependent NJ-ODEs to Noisy Observations and a Dependent Observation Framework

The Path-Dependent Neural Jump ODE (PD-NJ-ODE) is a model for predicting continuous-time stochastic processes with irregular and incomplete observations. In particular, the method learns optimal forecasts given irregularly sampled time series of incomplete past observations. So far the process itself and the coordinate-wise observation times were assumed to be independent and observations were assumed to be noiseless. In this work we discuss two extensions to lift these restrictions and provide theoretical guarantees as well as empirical examples for them.

How (Implicit) Regularization of ReLU Neural Networks Characterizes the Learned Function -- Part II: the Multi-D Case of Two Layers with Random First Layer

Randomized neural networks (randomized NNs), where only the terminal layer's weights are optimized constitute a powerful model class to reduce computational time in training the neural network model. At the same time, these models generalize surprisingly well in various regression and classification tasks. In this paper, we give an exact macroscopic characterization (i.e., a characterization in function space) of the generalization behavior of randomized, shallow NNs with ReLU activation (RSNs). We show that RSNs correspond to a generalized additive model (GAM)-typed regression in which infinitely many directions are considered: the infinite generalized additive model (IGAM). The IGAM is formalized as solution to an optimization problem in function space for a specific regularization functional and a fairly general loss. This work is an extension to multivariate NNs of prior work, where we showed how wide RSNs with ReLU activation behave like spline regression under certain conditions and if the input is one-dimensional.

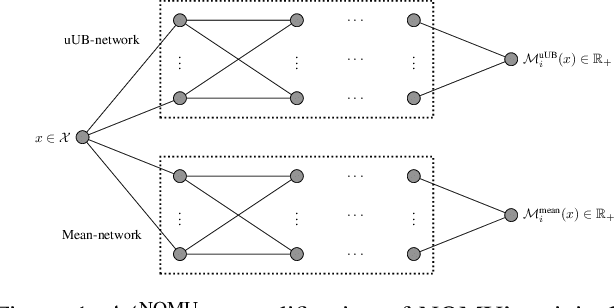
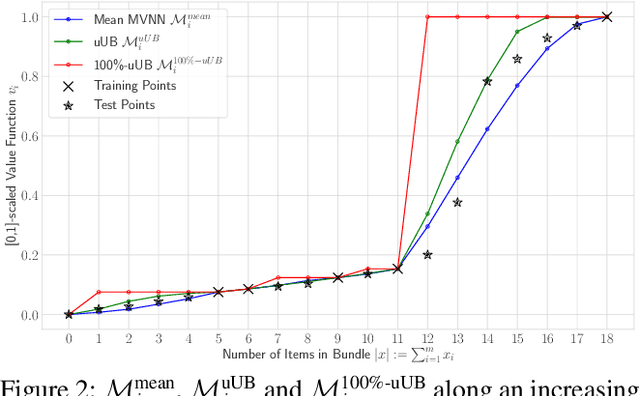
Bayesian Optimization-based Combinatorial Assignment

We study the combinatorial assignment domain, which includes combinatorial auctions and course allocation. The main challenge in this domain is that the bundle space grows exponentially in the number of items. To address this, several papers have recently proposed machine learning-based preference elicitation algorithms that aim to elicit only the most important information from agents. However, the main shortcoming of this prior work is that it does not model a mechanism's uncertainty over values for not yet elicited bundles. In this paper, we address this shortcoming by presenting a Bayesian Optimization-based Combinatorial Assignment (BOCA) mechanism. Our key technical contribution is to integrate a method for capturing model uncertainty into an iterative combinatorial auction mechanism. Concretely, we design a new method for estimating an upper uncertainty bound that can be used as an acquisition function to determine the next query to the agents. This enables the mechanism to properly explore (and not just exploit) the bundle space during its preference elicitation phase. We run computational experiments in several spectrum auction domains to evaluate BOCA's performance. Our results show that BOCA achieves higher allocative efficiency than state-of-the-art approaches.

Infinite width (finite depth) neural networks benefit from multi-task learning unlike shallow Gaussian Processes -- an exact quantitative macroscopic characterization

We prove in this paper that optimizing wide ReLU neural networks (NNs) with at least one hidden layer using l2-regularization on the parameters enforces multi-task learning due to representation-learning - also in the limit of width to infinity. This is in contrast to multiple other results in the literature, in which idealized settings are assumed and where wide (ReLU)-NNs loose their ability to benefit from multi-task learning in the infinite width limit. We deduce the ability of multi-task learning from proving an exact quantitative macroscopic characterization of the learned NN in an appropriate function space.

NOMU: Neural Optimization-based Model Uncertainty

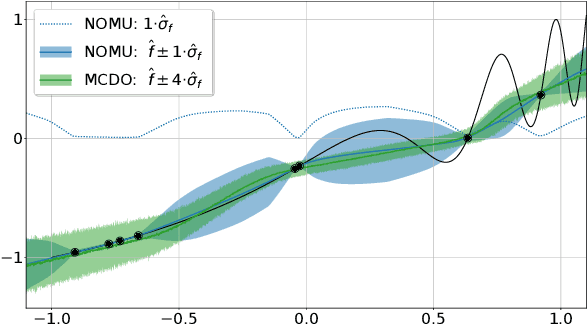
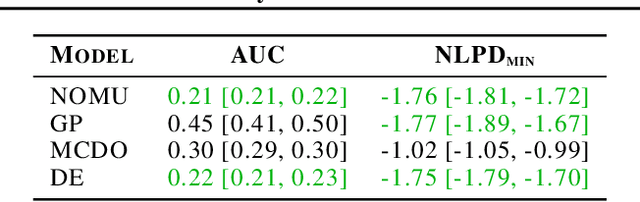
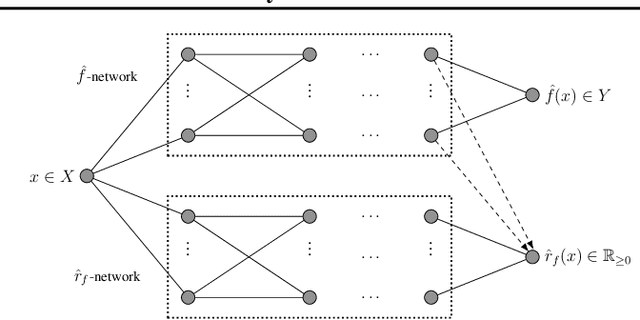
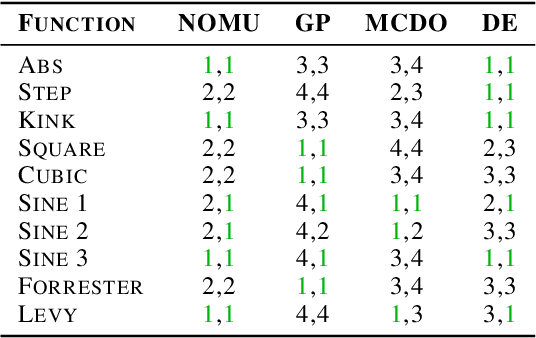
We introduce a new approach for capturing model uncertainty for neural networks (NNs) in regression, which we call Neural Optimization-based Model Uncertainty (NOMU). The main idea of NOMU is to design a network architecture consisting of two connected sub-networks, one for the model prediction and one for the model uncertainty, and to train it using a carefully designed loss function. With this design, NOMU can provide model uncertainty for any given (previously trained) NN by plugging it into the framework as the sub-network used for model prediction. NOMU is designed to yield uncertainty bounds (UBs) that satisfy four important desiderata regarding model uncertainty, which established methods often do not satisfy. Furthermore, our UBs are themselves representable as a single NN, which leads to computational cost advantages in applications such as Bayesian optimization. We evaluate NOMU experimentally in multiple settings. For regression, we show that NOMU performs as well as or better than established benchmarks. For Bayesian optimization, we show that NOMU outperforms all other benchmarks.

How implicit regularization of Neural Networks affects the learned function -- Part I

Today, various forms of neural networks are trained to perform approximation tasks in many fields. However, the solutions obtained are not wholly understood. Empirical results suggest that the training favors regularized solutions. These observations motivate us to analyze properties of the solutions found by the gradient descent algorithm frequently employed to perform the training task. As a starting point, we consider one dimensional (shallow) neural networks in which weights are chosen randomly and only the terminal layer is trained. We show, that the resulting solution converges to the smooth spline interpolation of the training data as the number of hidden nodes tends to infinity. This might give valuable insight on the properties of the solutions obtained using gradient descent methods in general settings.