Optimal Stopping via Randomized Neural Networks

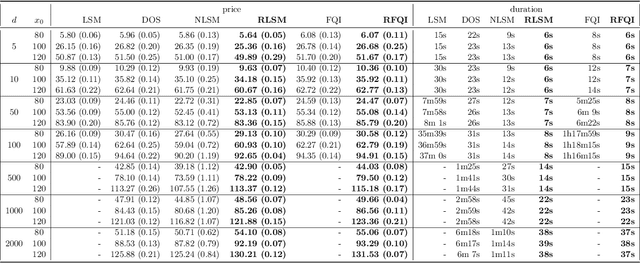
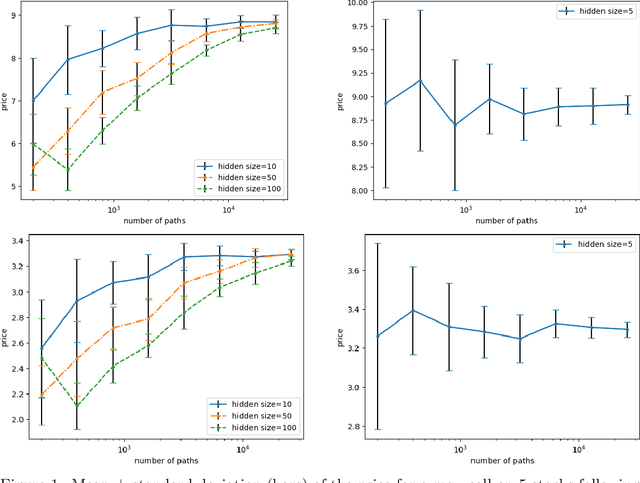
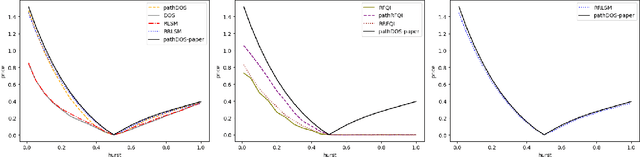
This paper presents new machine learning approaches to approximate the solution of optimal stopping problems. The key idea of these methods is to use neural networks, where the hidden layers are generated randomly and only the last layer is trained, in order to approximate the continuation value. Our approaches are applicable for high dimensional problems where the existing approaches become increasingly impractical. In addition, since our approaches can be optimized using a simple linear regression, they are very easy to implement and theoretical guarantees can be provided. In Markovian examples our randomized reinforcement learning approach and in non-Markovian examples our randomized recurrent neural network approach outperform the state-of-the-art and other relevant machine learning approaches.

Theoretical Guarantees for Learning Conditional Expectation using Controlled ODE-RNN

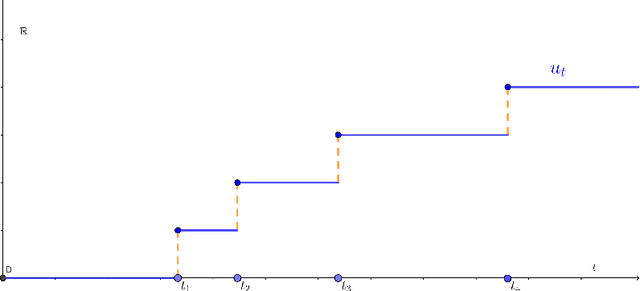
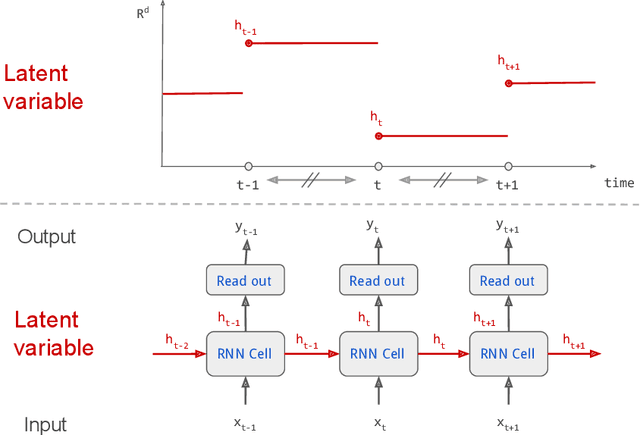
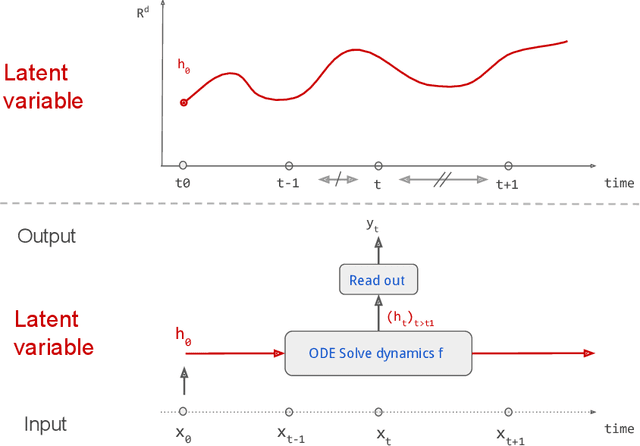
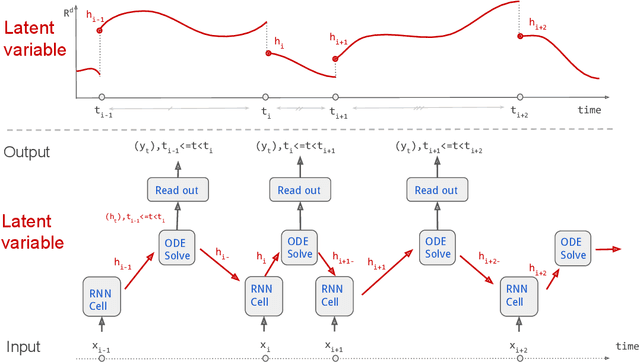
Continuous stochastic processes are widely used to model time series that exhibit a random behaviour. Predictions of the stochastic process can be computed by the conditional expectation given the current information. To this end, we introduce the controlled ODE-RNN that provides a data-driven approach to learn the conditional expectation of a stochastic process. Our approach extends the ODE-RNN framework which models the latent state of a recurrent neural network (RNN) between two observations with a neural ordinary differential equation (neural ODE). We show that controlled ODEs provide a general framework which can in particular describe the ODE-RNN, combining in a single equation the continuous neural ODE part with the jumps introduced by RNN. We demonstrate the predictive capabilities of this model by proving that, under some regularities assumptions, the output process converges to the conditional expectation process.

Denise: Deep Learning based Robust PCA for Positive Semidefinite Matrices

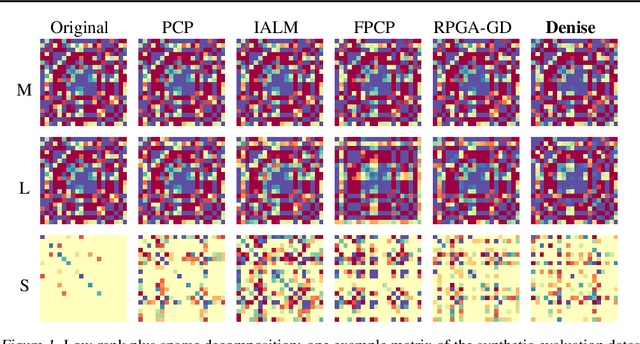
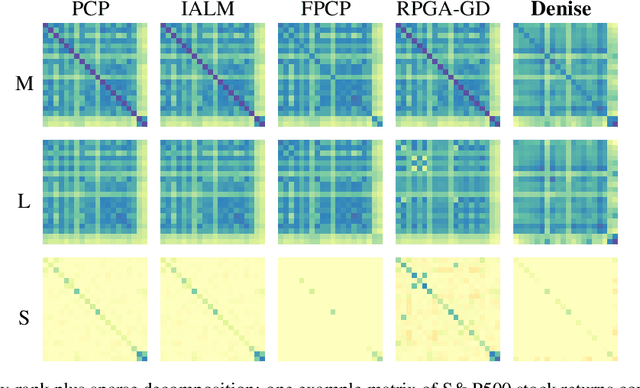
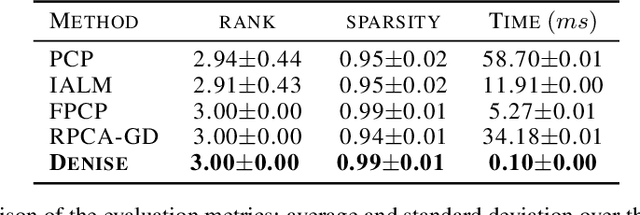
We introduce Denise, a deep learning based algorithm for decomposing positive semidefinite matrices into the sum of a low rank plus a sparse matrix. The deep neural network is trained on a randomly generated dataset using the Cholesky factorization. This method, benchmarked on synthetic datasets as well as on some S&P500 stock returns covariance matrices, achieves comparable results to several state-of-the-art techniques, while outperforming all existing algorithms in terms of computational time. Finally, theoretical results concerning the convergence of the training are derived.

Estimating Full Lipschitz Constants of Deep Neural Networks

We estimate the Lipschitz constants of the gradient of a deep neural network and the network itself with respect to the full set of parameters. We first develop estimates for a deep feed-forward densely connected network and then, in a more general framework, for all neural networks that can be represented as solutions of controlled ordinary differential equations, where time appears as continuous depth. These estimates can be used to set the step size of stochastic gradient descent methods, which is illustrated for one example method.