Diverse Approaches to Optimal Execution Schedule Generation

We present the first application of MAP-Elites, a quality-diversity algorithm, to trade execution. Rather than searching for a single optimal policy, MAP-Elites generates a diverse portfolio of regime-specialist strategies indexed by liquidity and volatility conditions. Individual specialists achieve 8-10% performance improvements within their behavioural niches, while other cells show degradation, suggesting opportunities for ensemble approaches that combine improved specialists with the baseline PPO policy. Results indicate that quality-diversity methods offer promise for regime-adaptive execution, though substantial computational resources per behavioural cell may be required for robust specialist development across all market conditions. To ensure experimental integrity, we develop a calibrated Gymnasium environment focused on order scheduling rather than tactical placement decisions. The simulator features a transient impact model with exponential decay and square-root volume scaling, fit to 400+ U.S. equities with R^2>0.02 out-of-sample. Within this environment, two Proximal Policy Optimization architectures - both MLP and CNN feature extractors - demonstrate substantial improvements over industry baselines, with the CNN variant achieving 2.13 bps arrival slippage versus 5.23 bps for VWAP on 4,900 out-of-sample orders ($21B notional). These results validate both the simulation realism and provide strong single-policy baselines for quality-diversity methods.

Learning with Expected Signatures: Theory and Applications

The expected signature maps a collection of data streams to a lower dimensional representation, with a remarkable property: the resulting feature tensor can fully characterize the data generating distribution. This "model-free" embedding has been successfully leveraged to build multiple domain-agnostic machine learning (ML) algorithms for time series and sequential data. The convergence results proved in this paper bridge the gap between the expected signature's empirical discrete-time estimator and its theoretical continuous-time value, allowing for a more complete probabilistic interpretation of expected signature-based ML methods. Moreover, when the data generating process is a martingale, we suggest a simple modification of the expected signature estimator with significantly lower mean squared error and empirically demonstrate how it can be effectively applied to improve predictive performance.

Deep Hedging: Continuous Reinforcement Learning for Hedging of General Portfolios across Multiple Risk Aversions

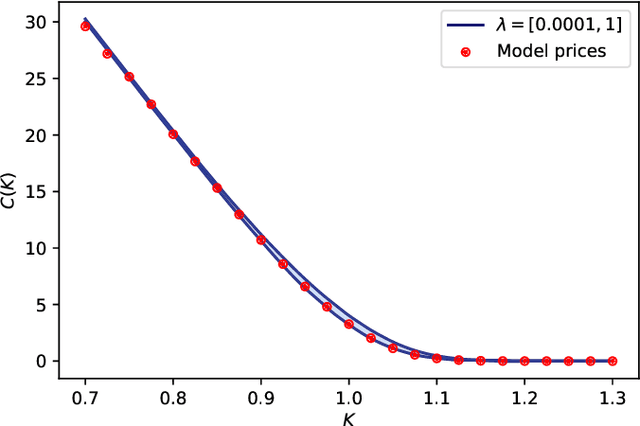
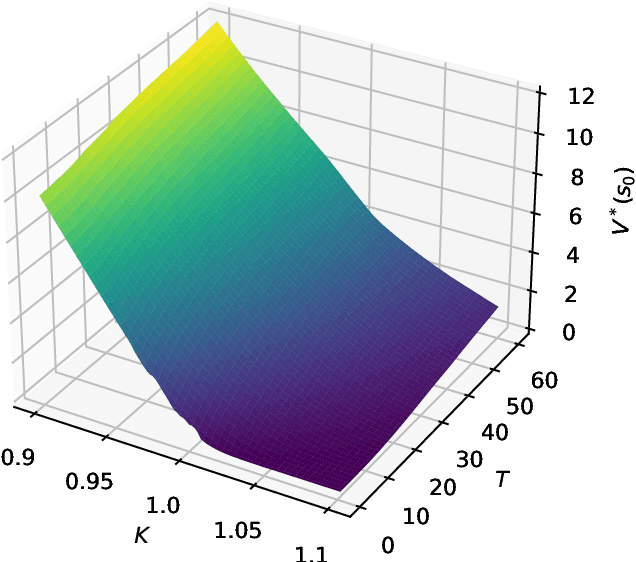
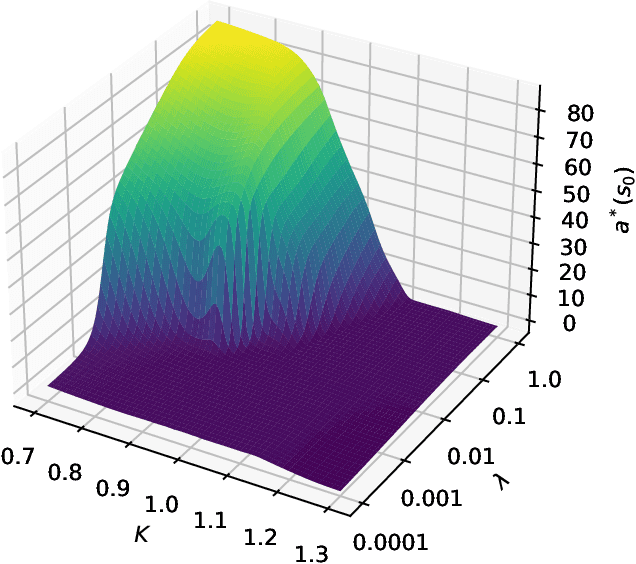
We present a method for finding optimal hedging policies for arbitrary initial portfolios and market states. We develop a novel actor-critic algorithm for solving general risk-averse stochastic control problems and use it to learn hedging strategies across multiple risk aversion levels simultaneously. We demonstrate the effectiveness of the approach with a numerical example in a stochastic volatility environment.

Deep Hedging: Learning to Remove the Drift under Trading Frictions with Minimal Equivalent Near-Martingale Measures

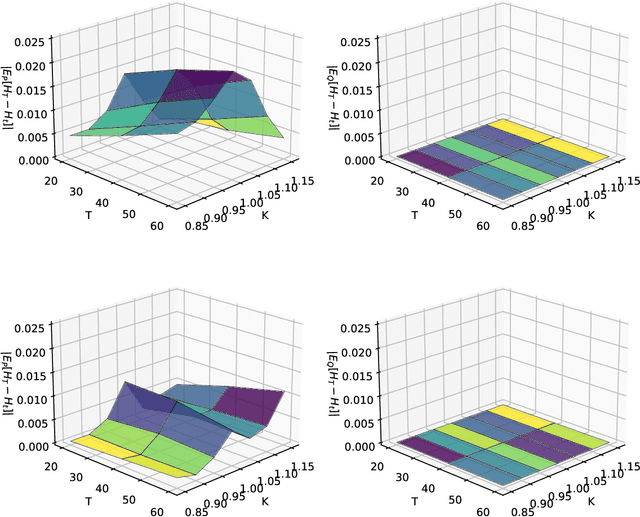
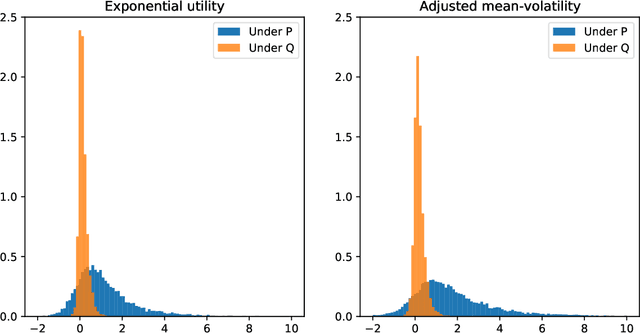
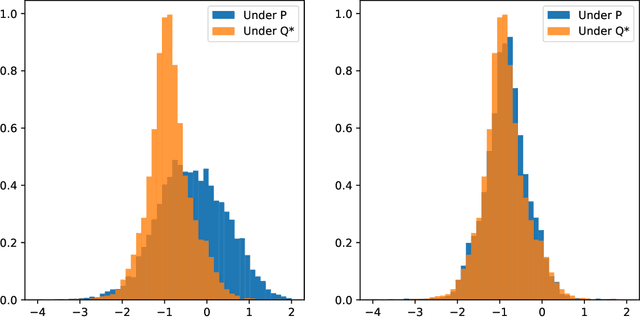
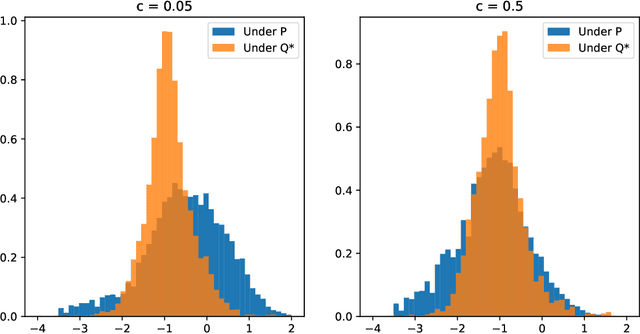
We present a numerically efficient approach for learning minimal equivalent martingale measures for market simulators of tradable instruments, e.g. for a spot price and options written on the same underlying. In the presence of transaction cost and trading restrictions, we relax the results to learning minimal equivalent "near-martingale measures" under which expected returns remain within prevailing bid/ask spreads. Our approach to thus "removing the drift" in a high dimensional complex space is entirely model-free and can be applied to any market simulator which does not exhibit classic arbitrage. The resulting model can be used for risk neutral pricing, or, in the case of transaction costs or trading constraints, for "Deep Hedging". We demonstrate our approach by applying it to two market simulators, an auto-regressive discrete-time stochastic implied volatility model, and a Generative Adversarial Network (GAN) based simulator, both of which trained on historical data of option prices under the statistical measure to produce realistic samples of spot and option prices. We comment on robustness with respect to estimation error of the original market simulator.

Deep Hedging: Learning Risk-Neutral Implied Volatility Dynamics

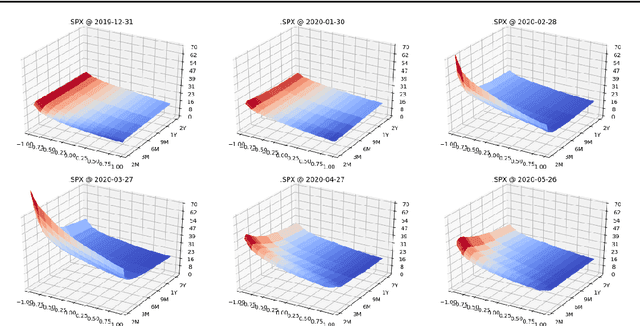
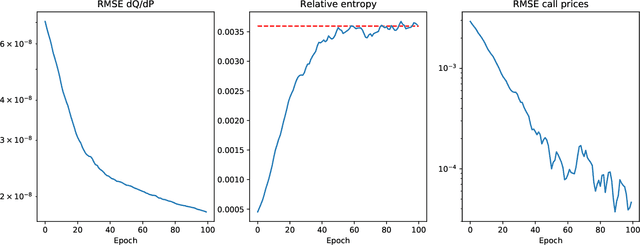
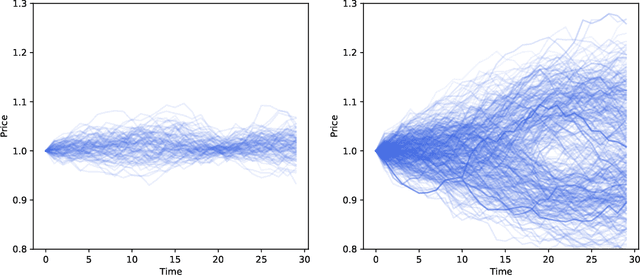
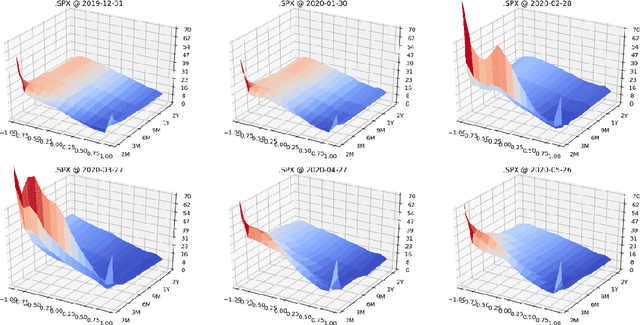
We present a numerically efficient approach for learning a risk-neutral measure for paths of simulated spot and option prices up to a finite horizon under convex transaction costs and convex trading constraints. This approach can then be used to implement a stochastic implied volatility model in the following two steps: 1. Train a market simulator for option prices, as discussed for example in our recent; 2. Find a risk-neutral density, specifically the minimal entropy martingale measure. The resulting model can be used for risk-neutral pricing, or for Deep Hedging in the case of transaction costs or trading constraints. To motivate the proposed approach, we also show that market dynamics are free from "statistical arbitrage" in the absence of transaction costs if and only if they follow a risk-neutral measure. We additionally provide a more general characterization in the presence of convex transaction costs and trading constraints. These results can be seen as an analogue of the fundamental theorem of asset pricing for statistical arbitrage under trading frictions and are of independent interest.