Using joint angles based on the international biomechanical standards for human action recognition and related tasks

Keypoint data has received a considerable amount of attention in machine learning for tasks like action detection and recognition. However, human experts in movement such as doctors, physiotherapists, sports scientists and coaches use a notion of joint angles standardised by the International Society of Biomechanics to precisely and efficiently communicate static body poses and movements. In this paper, we introduce the basic biomechanical notions and show how they can be used to convert common keypoint data into joint angles that uniquely describe the given pose and have various desirable mathematical properties, such as independence of both the camera viewpoint and the person performing the action. We experimentally demonstrate that the joint angle representation of keypoint data is suitable for machine learning applications and can in some cases bring an immediate performance gain. The use of joint angles as a human meaningful representation of kinematic data is in particular promising for applications where interpretability and dialog with human experts is important, such as many sports and medical applications. To facilitate further research in this direction, we will release a python package to convert keypoint data into joint angles as outlined in this paper.

Logsig-RNN: a novel network for robust and efficient skeleton-based action recognition

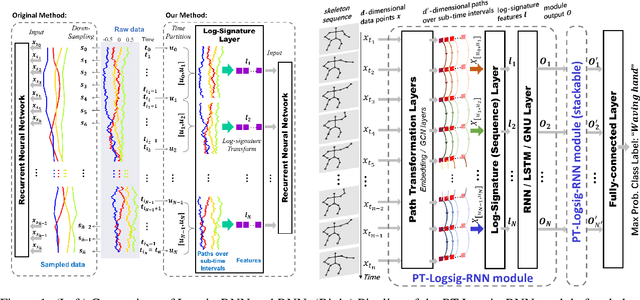
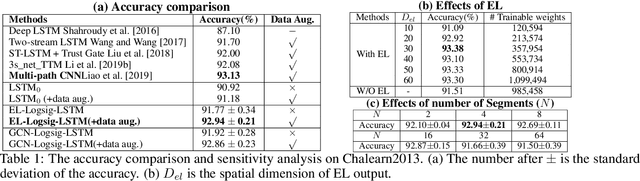
This paper contributes to the challenge of skeleton-based human action recognition in videos. The key step is to develop a generic network architecture to extract discriminative features for the spatio-temporal skeleton data. In this paper, we propose a novel module, namely Logsig-RNN, which is the combination of the log-signature layer and recurrent type neural networks (RNNs). The former one comes from the mathematically principled technology of signatures and log-signatures as representations for streamed data, which can manage high sample rate streams, non-uniform sampling and time series of variable length. It serves as an enhancement of the recurrent layer, which can be conveniently plugged into neural networks. Besides we propose two path transformation layers to significantly reduce path dimension while retaining the essential information fed into the Logsig-RNN module. Finally, numerical results demonstrate that replacing the RNN module by the Logsig-RNN module in SOTA networks consistently improves the performance on both Chalearn gesture data and NTU RGB+D 120 action data in terms of accuracy and robustness. In particular, we achieve the state-of-the-art accuracy on Chalearn2013 gesture data by combining simple path transformation layers with the Logsig-RNN. Codes are available at https://github.com/steveliao93/GCN_LogsigRNN.

Approximate Representer Theorems in Non-reflexive Banach Spaces

The representer theorem is one of the most important mathematical foundations for regularised learning and kernel methods. Classical formulations of the theorem state sufficient conditions under which a regularisation problem on a Hilbert space admits a solution in the subspace spanned by the representers of the data points. This turns the problem into an equivalent optimisation problem in a finite dimensional space, making it computationally tractable. Moreover, Banach space methods for learning have been receiving more and more attention. Considering the representer theorem in Banach spaces is hence of increasing importance. Recently the question of the necessary condition for a representer theorem to hold in Hilbert spaces and certain Banach spaces has been considered. It has been shown that a classical representer theorem cannot exist in general in non-reflexive Banach spaces. In this paper we propose a notion of approximate solutions and approximate representer theorem to overcome this problem. We show that for these notions we can indeed extend the previous results to obtain a unified theory for the existence of representer theorems in any general Banach spaces, in particular including $l_1$-type spaces. We give a precise characterisation when a regulariser admits a classical representer theorem and when only an approximate representer theorem is possible.

When is there a Representer Theorem? Reflexive Banach spaces

We consider a general regularised interpolation problem for learning a parameter vector from data. The well known representer theorem says that under certain conditions on the regulariser there exists a solution in the linear span of the data points. This is the core of kernel methods in machine learning as it makes the problem computationally tractable. Most literature deals only with sufficient conditions for representer theorems in Hilbert spaces. We prove necessary and sufficient conditions for the existence of representer theorems in reflexive Banach spaces and illustrate why in a sense reflexivity is the minimal requirement on the function space. We further show that if the learning relies on the linear representer theorem the solution is independent of the regulariser and in fact determined by the function space alone. This in particular shows the value of generalising Hilbert space learning theory to Banach spaces.

When is there a Representer Theorem? Nondifferentiable Regularisers and Banach spaces

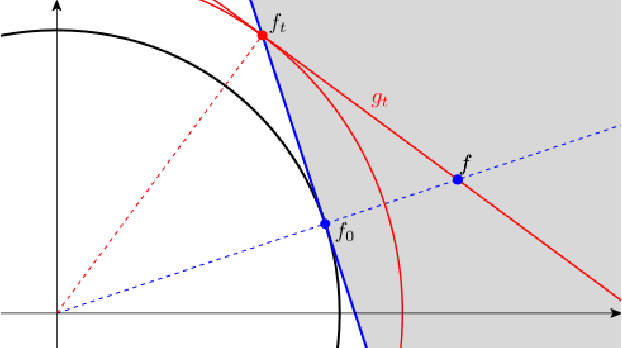
We consider a general regularised interpolation problem for learning a parameter vector from data. The well known representer theorem says that under certain conditions on the regulariser there exists a solution in the linear span of the data points. This is the core of kernel methods in machine learning as it makes the problem computationally tractable. Necessary and sufficient conditions for differentiable regularisers on Hilbert spaces to admit a representer theorem have been proved. We extend those results to nondifferentiable regularisers on uniformly convex and uniformly smooth Banach spaces. This gives a (more) complete answer to the question when there is a representer theorem. We then note that for regularised interpolation in fact the solution is determined by the function space alone and independent of the regulariser, making the extension to Banach spaces even more valuable.