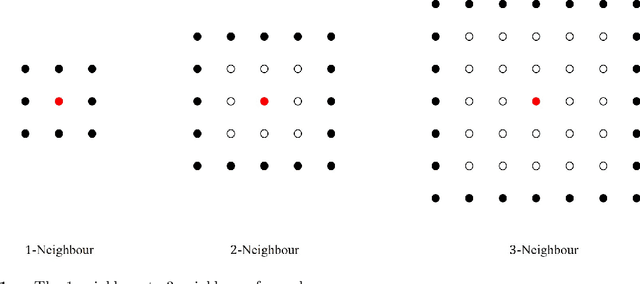
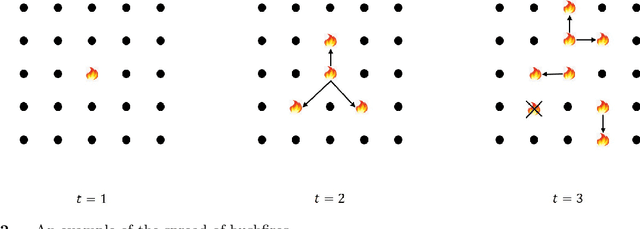
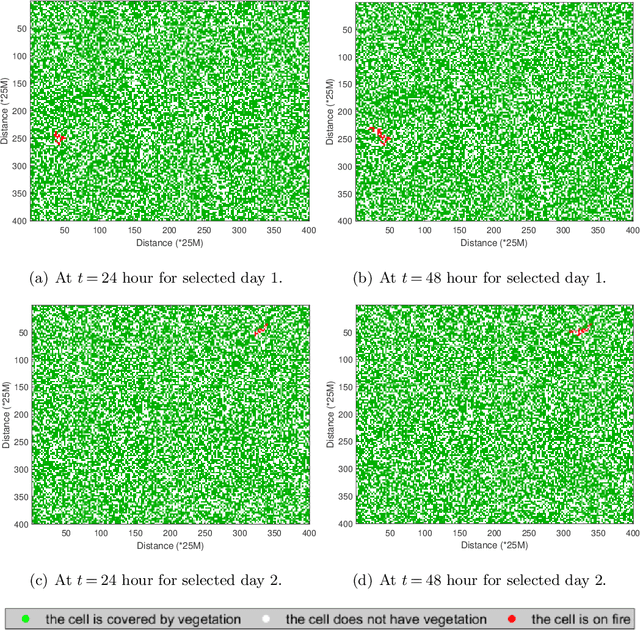
Online Planning of Power Flows for Power Systems Against Bushfires Using Spatial Context

The 2019-20 Australia bushfire incurred numerous economic losses and significantly affected the operations of power systems. A power station or transmission line can be significantly affected due to bushfires, leading to an increase in operational costs. We study a fundamental but challenging problem of planning the optimal power flow (OPF) for power systems subject to bushfires. Considering the stochastic nature of bushfire spread, we develop a model to capture such dynamics based on Moore's neighborhood model. Under a periodic inspection scheme that reveals the in-situ bushfire status, we propose an online optimization modeling framework that sequentially plans the power flows in the electricity network. Our framework assumes that the spread of bushfires is non-stationary over time, and the spread and containment probabilities are unknown. To meet these challenges, we develop a contextual online learning algorithm that treats the in-situ geographical information of the bushfire as a 'spatial context'. The online learning algorithm learns the unknown probabilities sequentially based on the observed data and then makes the OPF decision accordingly. The sequential OPF decisions aim to minimize the regret function, which is defined as the cumulative loss against the clairvoyant strategy that knows the true model parameters. We provide a theoretical guarantee of our algorithm by deriving a bound on the regret function, which outperforms the regret bound achieved by other benchmark algorithms. Our model assumptions are verified by the real bushfire data from NSW, Australia, and we apply our model to two power systems to illustrate its applicability.

Pricing with Contextual Elasticity and Heteroscedastic Valuation

We study an online contextual dynamic pricing problem, where customers decide whether to purchase a product based on its features and price. We introduce a novel approach to modeling a customer's expected demand by incorporating feature-based price elasticity, which can be equivalently represented as a valuation with heteroscedastic noise. To solve the problem, we propose a computationally efficient algorithm called "Pricing with Perturbation (PwP)", which enjoys an $O(\sqrt{dT\log T})$ regret while allowing arbitrary adversarial input context sequences. We also prove a matching lower bound at $\Omega(\sqrt{dT})$ to show the optimality regarding $d$ and $T$ (up to $\log T$ factors). Our results shed light on the relationship between contextual elasticity and heteroscedastic valuation, providing insights for effective and practical pricing strategies.

TheoremQA: A Theorem-driven Question Answering dataset

The recent LLMs like GPT-4 and PaLM-2 have made tremendous progress in solving fundamental math problems like GSM8K by achieving over 90% accuracy. However, their capabilities to solve more challenging math problems which require domain-specific knowledge (i.e. theorem) have yet to be investigated. In this paper, we introduce TheoremQA, the first theorem-driven question-answering dataset designed to evaluate AI models' capabilities to apply theorems to solve challenging science problems. TheoremQA is curated by domain experts containing 800 high-quality questions covering 350 theorems (e.g. Taylor's theorem, Lagrange's theorem, Huffman coding, Quantum Theorem, Elasticity Theorem, etc) from Math, Physics, EE&CS, and Finance. We evaluate a wide spectrum of 16 large language and code models with different prompting strategies like Chain-of-Thoughts and Program-of-Thoughts. We found that GPT-4's capabilities to solve these problems are unparalleled, achieving an accuracy of 51% with Program-of-Thoughts Prompting. All the existing open-sourced models are below 15%, barely surpassing the random-guess baseline. Given the diversity and broad coverage of TheoremQA, we believe it can be used as a better benchmark to evaluate LLMs' capabilities to solve challenging science problems. The data and code are released in https://github.com/wenhuchen/TheoremQA.

Doubly Fair Dynamic Pricing

We study the problem of online dynamic pricing with two types of fairness constraints: a "procedural fairness" which requires the proposed prices to be equal in expectation among different groups, and a "substantive fairness" which requires the accepted prices to be equal in expectation among different groups. A policy that is simultaneously procedural and substantive fair is referred to as "doubly fair". We show that a doubly fair policy must be random to have higher revenue than the best trivial policy that assigns the same price to different groups. In a two-group setting, we propose an online learning algorithm for the 2-group pricing problems that achieves $\tilde{O}(\sqrt{T})$ regret, zero procedural unfairness and $\tilde{O}(\sqrt{T})$ substantive unfairness over $T$ rounds of learning. We also prove two lower bounds showing that these results on regret and unfairness are both information-theoretically optimal up to iterated logarithmic factors. To the best of our knowledge, this is the first dynamic pricing algorithm that learns to price while satisfying two fairness constraints at the same time.

Towards Agnostic Feature-based Dynamic Pricing: Linear Policies vs Linear Valuation with Unknown Noise

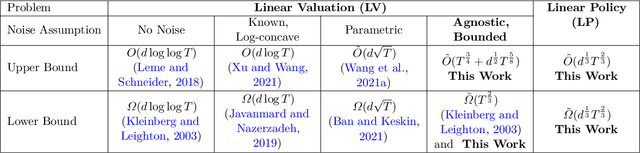
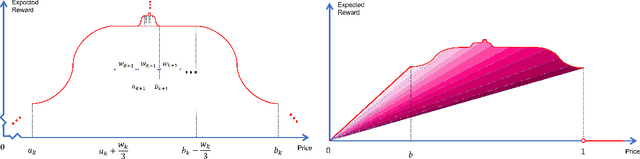
In feature-based dynamic pricing, a seller sets appropriate prices for a sequence of products (described by feature vectors) on the fly by learning from the binary outcomes of previous sales sessions ("Sold" if valuation $\geq$ price, and "Not Sold" otherwise). Existing works either assume noiseless linear valuation or precisely-known noise distribution, which limits the applicability of those algorithms in practice when these assumptions are hard to verify. In this work, we study two more agnostic models: (a) a "linear policy" problem where we aim at competing with the best linear pricing policy while making no assumptions on the data, and (b) a "linear noisy valuation" problem where the random valuation is linear plus an unknown and assumption-free noise. For the former model, we show a $\tilde{\Theta}(d^{\frac13}T^{\frac23})$ minimax regret up to logarithmic factors. For the latter model, we present an algorithm that achieves an $\tilde{O}(T^{\frac34})$ regret, and improve the best-known lower bound from $\Omega(T^{\frac35})$ to $\tilde{\Omega}(T^{\frac23})$. These results demonstrate that no-regret learning is possible for feature-based dynamic pricing under weak assumptions, but also reveal a disappointing fact that the seemingly richer pricing feedback is not significantly more useful than the bandit-feedback in regret reduction.

Logarithmic Regret in Feature-based Dynamic Pricing

Feature-based dynamic pricing is an increasingly popular model of setting prices for highly differentiated products with applications in digital marketing, online sales, real estate and so on. The problem was formally studied as an online learning problem (Cohen et al., 2016; Javanmard & Nazerzadeh, 2019) where a seller needs to propose prices on the fly for a sequence of $T$ products based on their features $x$ while having a small regret relative to the best -- "omniscient" -- pricing strategy she could have come up with in hindsight. We revisit this problem and provide two algorithms (EMLP and ONSP) for stochastic and adversarial feature settings, respectively, and prove the optimal $O(d\log{T})$ regret bounds for both. In comparison, the best existing results are $O\left(\min\left\{\frac{1}{\lambda_{\min}^2}\log{T}, \sqrt{T}\right\}\right)$ and $O(T^{2/3})$ respectively, with $\lambda_{\min}$ being the smallest eigenvalue of $\mathbb{E}[xx^T]$ that could be arbitrarily close to $0$. We also prove an $\Omega(\sqrt{T})$ information-theoretic lower bound for a slightly more general setting, which demonstrates that "knowing-the-demand-curve" leads to an exponential improvement in feature-based dynamic pricing.