TrustMol: Trustworthy Inverse Molecular Design via Alignment with Molecular Dynamics

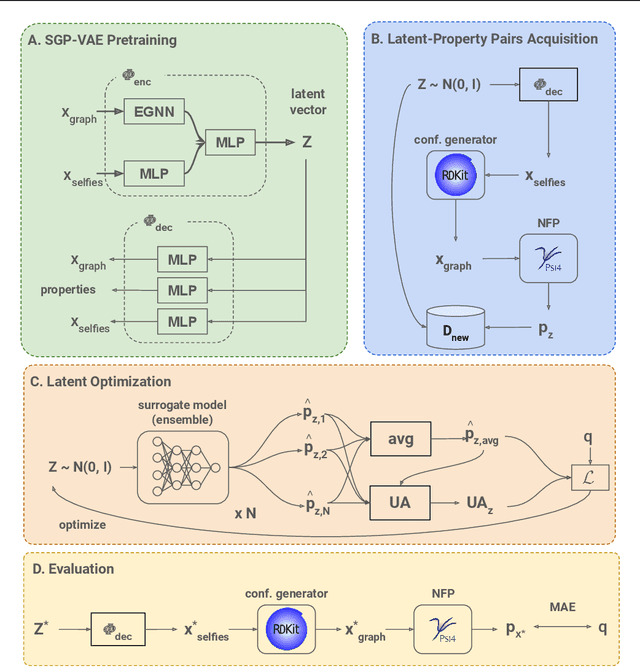
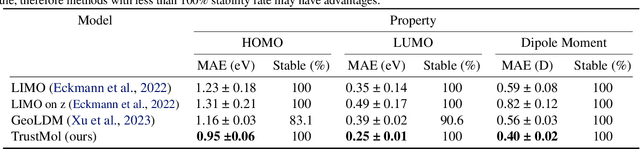
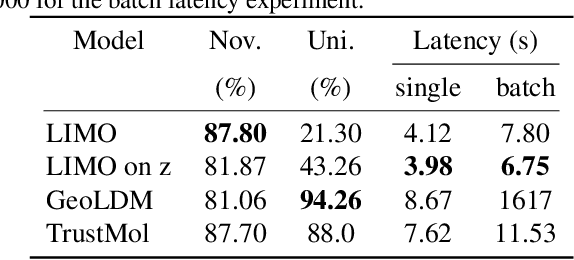
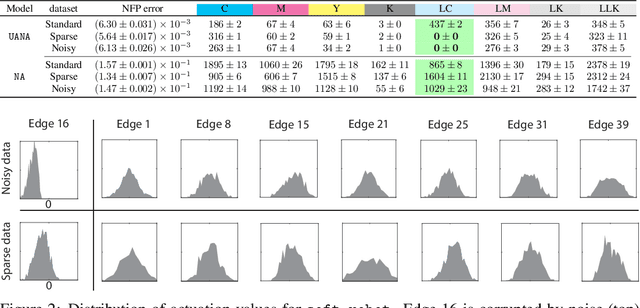
Data-driven generation of molecules with desired properties, also known as inverse molecular design (IMD), has attracted significant attention in recent years. Despite the significant progress in the accuracy and diversity of solutions, existing IMD methods lag behind in terms of trustworthiness. The root issue is that the design process of these methods is increasingly more implicit and indirect, and this process is also isolated from the native forward process (NFP), the ground-truth function that models the molecular dynamics. Following this insight, we propose TrustMol, an IMD method built to be trustworthy. For this purpose, TrustMol relies on a set of technical novelties including a new variational autoencoder network. Moreover, we propose a latent-property pairs acquisition method to effectively navigate the complexities of molecular latent optimization, a process that seems intuitive yet challenging due to the high-frequency and discontinuous nature of molecule space. TrustMol also integrates uncertainty-awareness into molecular latent optimization. These lead to improvements in both explainability and reliability of the IMD process. We validate the trustworthiness of TrustMol through a wide range of experiments.

Large-Batch, Neural Multi-Objective Bayesian Optimization

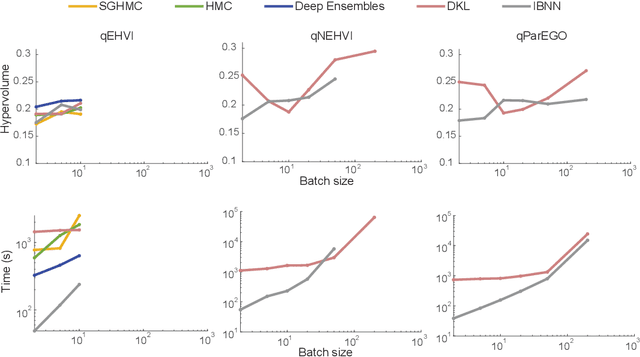
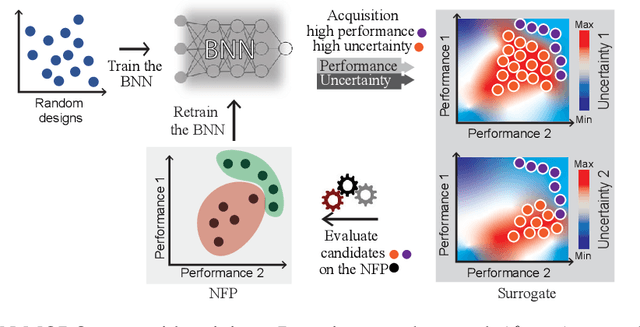
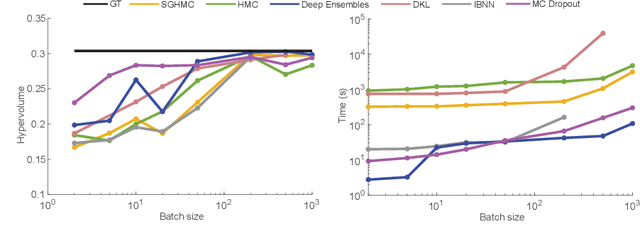
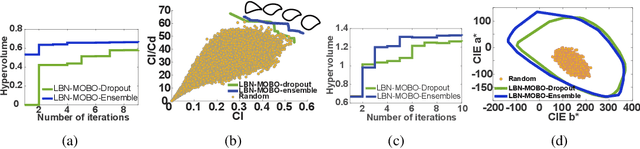
Bayesian optimization provides a powerful framework for global optimization of black-box, expensive-to-evaluate functions. However, it has a limited capacity in handling data-intensive problems, especially in multi-objective settings, due to the poor scalability of default Gaussian Process surrogates. We present a novel Bayesian optimization framework specifically tailored to address these limitations. Our method leverages a Bayesian neural networks approach for surrogate modeling. This enables efficient handling of large batches of data, modeling complex problems, and generating the uncertainty of the predictions. In addition, our method incorporates a scalable, uncertainty-aware acquisition strategy based on the well-known, easy-to-deploy NSGA-II. This fully parallelizable strategy promotes efficient exploration of uncharted regions. Our framework allows for effective optimization in data-intensive environments with a minimum number of iterations. We demonstrate the superiority of our method by comparing it with state-of-the-art multi-objective optimizations. We perform our evaluation on two real-world problems - airfoil design and color printing - showcasing the applicability and efficiency of our approach. Code is available at: https://github.com/an-on-ym-ous/lbn_mobo

Autoinverse: Uncertainty Aware Inversion of Neural Networks

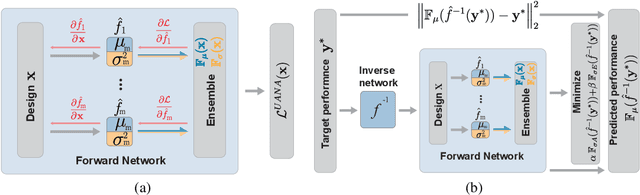
Neural networks are powerful surrogates for numerous forward processes. The inversion of such surrogates is extremely valuable in science and engineering. The most important property of a successful neural inverse method is the performance of its solutions when deployed in the real world, i.e., on the native forward process (and not only the learned surrogate). We propose Autoinverse, a highly automated approach for inverting neural network surrogates. Our main insight is to seek inverse solutions in the vicinity of reliable data which have been sampled form the forward process and used for training the surrogate model. Autoinverse finds such solutions by taking into account the predictive uncertainty of the surrogate and minimizing it during the inversion. Apart from high accuracy, Autoinverse enforces the feasibility of solutions, comes with embedded regularization, and is initialization free. We verify our proposed method through addressing a set of real-world problems in control, fabrication, and design.

Mixed Integer Neural Inverse Design

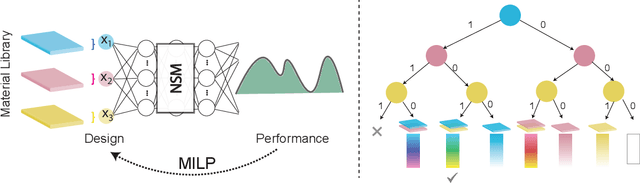
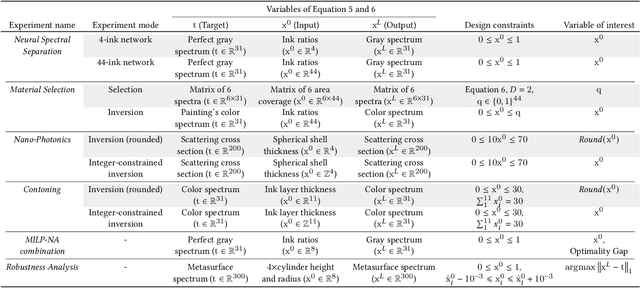
In computational design and fabrication, neural networks are becoming important surrogates for bulky forward simulations. A long-standing, intertwined question is that of inverse design: how to compute a design that satisfies a desired target performance? Here, we show that the piecewise linear property, very common in everyday neural networks, allows for an inverse design formulation based on mixed-integer linear programming. Our mixed-integer inverse design uncovers globally optimal or near optimal solutions in a principled manner. Furthermore, our method significantly facilitates emerging, but challenging, combinatorial inverse design tasks, such as material selection. For problems where finding the optimal solution is not desirable or tractable, we develop an efficient yet near-optimal hybrid optimization. Eventually, our method is able to find solutions provably robust to possible fabrication perturbations among multiple designs with similar performances.