Mixed Integer Neural Inverse Design
Paper and Code
Sep 27, 2021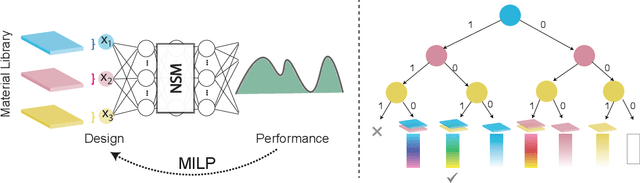



In computational design and fabrication, neural networks are becoming important surrogates for bulky forward simulations. A long-standing, intertwined question is that of inverse design: how to compute a design that satisfies a desired target performance? Here, we show that the piecewise linear property, very common in everyday neural networks, allows for an inverse design formulation based on mixed-integer linear programming. Our mixed-integer inverse design uncovers globally optimal or near optimal solutions in a principled manner. Furthermore, our method significantly facilitates emerging, but challenging, combinatorial inverse design tasks, such as material selection. For problems where finding the optimal solution is not desirable or tractable, we develop an efficient yet near-optimal hybrid optimization. Eventually, our method is able to find solutions provably robust to possible fabrication perturbations among multiple designs with similar performances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge